题目内容
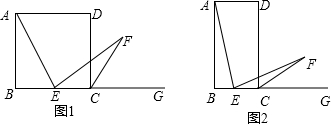
如图1,四边形ABCD是正方形,G在BC的延长线上,点E是边BC上的任意一点(不与B、C重合),∠AEF=90°,且AE=EF,连接CF.(1)求证:∠FCG=45°;
(2)如图2,当四边形ABCD是矩形,且AB=2AD时,点E是边BC上的任意一点(不与B、C重合),∠AEF=90°,且AE=2EF,连接CF,求tan∠FCG的值.
分析:(1)连接FH,证出△ABE≌△EHF,得到BE=HF,再根据正四边形的性质得到BC=AB=EH,从而计算出EH-EC=BC-EC,即BE=CH,故CH=HF,再根据∠CHF=90°,求出∠FCG=45°;
(2)作FI⊥EG与I,证出△ABE∽△EIF,得到EI=AD=BC,求出tan∠FCG的值.
(2)作FI⊥EG与I,证出△ABE∽△EIF,得到EI=AD=BC,求出tan∠FCG的值.
解答:解:作FH⊥CG与H.
∵∠AEF=90°,
∴∠AEB+∠FEH=90°,
又∵∠BAE+∠AEB=90°,
∴∠FEH=∠EAB,
又∵∠B=∠EHF,
且AE=EF,
∴△ABE≌△EHF,
∴BE=HF,
BC=AB=EH,
∴EH-EC=BC-EC,
∴BE=CH,
∴CH=HF.
∴∠FCH=∠CFH=
=45°;
(2)作FI⊥EG与I.
∵∠AEF=90°,
∴∠AEB+∠FEI=90°,
又∵∠BAE+∠AEB=90°,
∴∠FEI=∠EAB,
又∵∠B=∠EIF,
∴△ABE∽△EIF,
∴
=
=
,
即EI=
AB,
故EI=AD=BC,
∴BE=CI,
∴tan∠FCG=
=
=
=
.

∵∠AEF=90°,
∴∠AEB+∠FEH=90°,
又∵∠BAE+∠AEB=90°,
∴∠FEH=∠EAB,
又∵∠B=∠EHF,
且AE=EF,
∴△ABE≌△EHF,
∴BE=HF,
BC=AB=EH,
∴EH-EC=BC-EC,
∴BE=CH,
∴CH=HF.
∴∠FCH=∠CFH=
| 180°-90° |
| 2 |
(2)作FI⊥EG与I.
∵∠AEF=90°,
∴∠AEB+∠FEI=90°,
又∵∠BAE+∠AEB=90°,
∴∠FEI=∠EAB,
又∵∠B=∠EIF,
∴△ABE∽△EIF,
∴
| EI |
| AB |
| EF |
| AE |
| 1 |
| 2 |
即EI=
| 1 |
| 2 |
故EI=AD=BC,
∴BE=CI,
∴tan∠FCG=
| FI |
| IC |
| FI |
| BE |
| FE |
| AB |
| 1 |
| 2 |

点评:此题考查了全等三角形与相似三角形的性质,巧妙运用正方形和矩形的性质,证明三角形全等或相似,是解题的关键.

练习册系列答案
相关题目
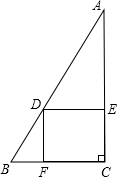 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.