题目内容
已知:在四边形ABCD中,AB=4cm,点E、F、G、H分别按A→B,B→C,C→D,D→A的方向同时出发,以1cm/秒的速度匀速运动,在运动过程中,设四边形EFGH的面积为S cm2,运动时间为t秒(0≤t≤4).
(1)当四边形ABCD为正方形时,如图1所示,
①求证:四边形EFGH是正方形;
②在某一时刻,把图1的四个直角三角形剪下来,拼成如图所示的正方形A1B1C1D1,且它的面积为10cm2.求中间正方形E1F1G1H1的面积.
(2)当四边形ABCD为菱形,且∠A=30°时,如图3所示.在运动过程中,四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.

(1)当四边形ABCD为正方形时,如图1所示,
①求证:四边形EFGH是正方形;
②在某一时刻,把图1的四个直角三角形剪下来,拼成如图所示的正方形A1B1C1D1,且它的面积为10cm2.求中间正方形E1F1G1H1的面积.
(2)当四边形ABCD为菱形,且∠A=30°时,如图3所示.在运动过程中,四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.

分析:(1)①根据题意,易得AE=BF=CG=DH,又由四边形ABCD是正方形,可得∠A=∠B=90°,AB=DA,进而可得四边形EFGH是菱形,又由∠BEF+∠BFE=90°,∠AEH=∠BFE可得∠FEH=90°,可证四边形EFGH是正方形;
②由正方形ABCD的边长为4cm,求出其面积,再由正方形A1B1C1D1的面积求出其边长,得到HE的长,求出正方形EFGH的面积,由正方形ABCD面积-正方形EFGH面积求出四个直角三角形的面积,由正方形A1B1C1D1的面积-四个直角三角形的面积即可得到中间正方形E1F1G1H1的面积;
(2)根据题意,易证△AEH≌△CGF,△EBF≌△GDH,作HM⊥AE于M,作FN⊥EB,交EB的延长线于N,设运动t秒后,四边形EFGH的面积S取最小值,则AE=t,AH=4-t,又在Rt△AMH中,∠HAM=30°,可得HM与AH的关系,四边形EFGH的面积与t的关系,其关系式为二次函数,由二次函数的性质,易得答案.
②由正方形ABCD的边长为4cm,求出其面积,再由正方形A1B1C1D1的面积求出其边长,得到HE的长,求出正方形EFGH的面积,由正方形ABCD面积-正方形EFGH面积求出四个直角三角形的面积,由正方形A1B1C1D1的面积-四个直角三角形的面积即可得到中间正方形E1F1G1H1的面积;
(2)根据题意,易证△AEH≌△CGF,△EBF≌△GDH,作HM⊥AE于M,作FN⊥EB,交EB的延长线于N,设运动t秒后,四边形EFGH的面积S取最小值,则AE=t,AH=4-t,又在Rt△AMH中,∠HAM=30°,可得HM与AH的关系,四边形EFGH的面积与t的关系,其关系式为二次函数,由二次函数的性质,易得答案.
解答: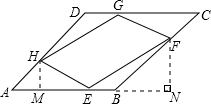 解:(1)①∵点E,F,G,H在四条边上的运动速度相同,
解:(1)①∵点E,F,G,H在四条边上的运动速度相同,
∴AE=BF=CG=DH,
∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=DA,
∴EB=HA,
在△AEH和△BFE中,
,
∴△AEH≌△BFE(SAS),
∴EH=FE(全等三角形的对应边相等),
同理可得:EH=FE=GF=HG,
∴四边形EFGH是菱形,
又∵∠BEF+∠BFE=90°,∠AEH=∠BFE,
∴∠BEF+∠AEH=90°,
∴∠FEH=90°,
∴四边形EFGH为正方形(有一个角是直角的菱形是正方形);
②∵正方形ABCD边长为4cm,正方形A1B1C1D1的面积为10cm2,
∴S正方形ABCD=16cm2,正方形A1B1C1D1的边长为
cm,即HE=
cm,
∴S正方形EFGH=10cm2,
∴S四个直角三角形=16-10=6cm2,
则正方形E1F1G1H1的面积S=10-6=4cm2;
(2)四边形EFGH的面积存在最小值,理由如下:
由条件,易证△AEH≌△CGF,△EBF≌△GDH,
作HM⊥AE于M,作FN⊥EB,交EB的延长线于N,
设运动t秒后,四边形EFGH的面积S取最小值,则AE=t,AH=4-t,
又在Rt△AMH中,∠HAM=30°,
∴HM=
AH=
(4-t),
同理可得FN=
BF=
t,
故S△AEH=
AE•HM=
t(4-t),S△EBF=
EB•FN=
t(4-t),
又S正方形ABCD=4×2=8,
∴四边形EFGH的面积S=8-4•
t(4-t)=t2-4t+8=(t-2)2+4,
当t=2秒时,四边形EFGH的面积取最小值等于4cm2.
 解:(1)①∵点E,F,G,H在四条边上的运动速度相同,
解:(1)①∵点E,F,G,H在四条边上的运动速度相同,∴AE=BF=CG=DH,
∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=DA,
∴EB=HA,
在△AEH和△BFE中,
|
∴△AEH≌△BFE(SAS),
∴EH=FE(全等三角形的对应边相等),
同理可得:EH=FE=GF=HG,
∴四边形EFGH是菱形,
又∵∠BEF+∠BFE=90°,∠AEH=∠BFE,
∴∠BEF+∠AEH=90°,
∴∠FEH=90°,
∴四边形EFGH为正方形(有一个角是直角的菱形是正方形);
②∵正方形ABCD边长为4cm,正方形A1B1C1D1的面积为10cm2,
∴S正方形ABCD=16cm2,正方形A1B1C1D1的边长为
| 10 |
| 10 |
∴S正方形EFGH=10cm2,
∴S四个直角三角形=16-10=6cm2,
则正方形E1F1G1H1的面积S=10-6=4cm2;
(2)四边形EFGH的面积存在最小值,理由如下:
由条件,易证△AEH≌△CGF,△EBF≌△GDH,
作HM⊥AE于M,作FN⊥EB,交EB的延长线于N,
设运动t秒后,四边形EFGH的面积S取最小值,则AE=t,AH=4-t,
又在Rt△AMH中,∠HAM=30°,
∴HM=
| 1 |
| 2 |
| 1 |
| 2 |
同理可得FN=
| 1 |
| 2 |
| 1 |
| 2 |
故S△AEH=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
又S正方形ABCD=4×2=8,
∴四边形EFGH的面积S=8-4•
| 1 |
| 4 |
当t=2秒时,四边形EFGH的面积取最小值等于4cm2.
点评:此题属于四边形综合题,涉及的知识有:全等三角形的判定与性质,正方形的判定与性质,二次函数的性质,含30度角三角形的面积,以及菱形的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目

 已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.
已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.
 如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.