题目内容
12.若三角形的周长为13,且三边均为整数,则满足条件的三角形有4种.分析 三角形的三边中,等边三角形三边相等;除此外,必有一边是最长边;然后首先确定第三边的取值范围,从而确定答案.
解答 解:设三边长分别为a≤b≤c,则a+b=13-c>c≥$\frac{13}{3}$,
∴$\frac{13}{3}$≤c<$\frac{13}{2}$,故c=5,或6;分类讨论如下:
①当c=5时,b=4,a=4或b=3,a=5;
②当c=6时,b=5,a=2或b=4,a=3;
∴满足条件的三角形的个数为4,
故答案为:4.
点评 本题考查了三角形的三边关系,属竞赛题型,且涉及分类讨论的思想.解答的关键是找到三边的取值范围及对三角形三边的理解把握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列说法正确的是( )
| A. | 能够完全重合的两个图形叫做全等图形 | |
| B. | 周长相等的三角形是全等三角形 | |
| C. | 各角相等的三角形是全等三角形 | |
| D. | 面积相等的三角形是全等三角形 |
20.直线y=5x+5和y=3x-1的交点必在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列各组线段中,能组成三角形的是( )
| A. | 4,6,10 | B. | 3,6,7 | C. | 5,6,12 | D. | 2,3,6 |
1.已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
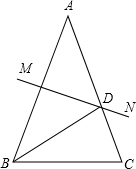 如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于30度.
如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于30度.