题目内容
3.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.(1)当∠MBN绕B点旋转到AE=CF时(如图1),若AE=1,试求AB的长;
(2)当∠MBN绕B点旋转到AE≠CF时,在图2这种情况下,求证AE+CF=EF;
(3)当∠MBN绕B点旋转到AE≠CF时,在图3这种情况下,(2)中结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请直接写出你的猜想.
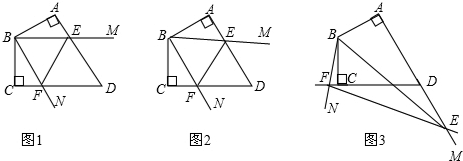
分析 (1)根据AE=CF可以求得BF=BE,易求得∠CBF=30°,即可解题;
(2)将Rt△ABE顺时针旋转120°,可得FG=CG+CF=AE+CF,易证∠GBF=∠EBF=60°,即可求证△GBF≌△EBF,可得FG=EF,即可解题;
(3)将Rt△ABE顺时针旋转120°,可得FG=CG-CF=AE-CF,易证∠GBF=∠EBF=60°,即可求证△GBF≌△EBF,可得FG=EF,即可解题.
解答 证明:(1)如图1中,
∵Rt△ABE和Rt△CBF中,AB=BC,CF=AE,
∴tan∠CBF=tan∠ABE,BF=BE,
∴∠CBF=∠ABE,
∵∠ABC=120°,∠MBN=60°,
∴∠CBF=30°,△BEF是等边三角形,
∵AE=CF=1,
∴AB=$\sqrt{3}$AE=$\sqrt{3}$
(2)如图2,将Rt△ABE顺时针旋转120°,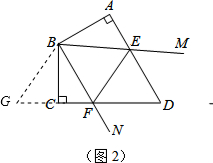
∵AB=BC,∠ABC=120°,
∴A点与C点重合,
∴BG=BE,FG=CG+CF=AE+CF,
∵∠ABC=120°,∠MBN=60°,∠ABE=∠CBG,
∴∠GBF=60°,
在△GBF和△EBF中,
$\left\{\begin{array}{l}{BG=BE}\\{∠GBF=∠EBF=60°}\\{BF=BF}\end{array}\right.$,
∴△GBF≌△EBF(SAS),
∴FG=EF,
∴EF=AE+CF;
(3)不成立,新结论为EF=AE-CF.
理由:如图3,将Rt△ABE顺时针旋转120°,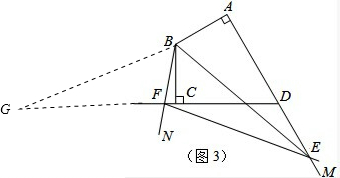
∵AB=BC,∠ABC=120°,
∴A点与C点重合,∠ABE=∠CBG,
∴BG=BE,FG=CG-CF=AE-CF,
∵∠ABC=∠ABE+∠CBE=120°,
∴∠CBG+∠CBE=∠GBE=120°,
∵∠MBN=60°,
∴∠GBF=60°,
在△BFG和△BFE中,
$\left\{\begin{array}{l}{BG=BE}\\{∠GBF=∠EBF=60°}\\{BF=BF}\end{array}\right.$,
∴△BFG≌△BFE,(SAS)
∴GF=EF,
∴EF=AE-CF.
点评 本题考查了全等三角形的判定和性质,30°角所对直角边是斜边一半的性质,等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,本题中求证△BFG≌△BFE是解题的关键.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | ax2+bx+c=0 |
| A. | 打开电视机正在播放欧洲杯 | |
| B. | 任意画一个三角形,其内角和为360° | |
| C. | 掷一枚质地均匀的骰子,掷出的点数为8 | |
| D. | 平行于同一条直线的两条直线平行 |
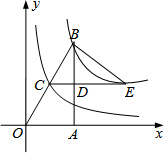 如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 与k1的值有关 |