题目内容
1．不等式组$\left\{{\begin{array}{l}{x-3＜0}\\{x+1≥0}\end{array}}\right.$的解集是-1≤x＜3．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：$\left\{{\begin{array}{l}{x-3＜0}\\{x+1≥0}\end{array}}\right.$，
解不等式x-3＜0，得：x＜3，
解不等式x+1≥0，得：x≥-1，
故不等式组的解集为：1≤x＜3，
故答案为：-1≤x＜3．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11．计算（a2）3的结果是（ ）
| A． | 3a2 | B． | 2a3 | C． | a5 | D． | a6 |
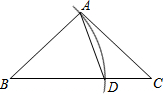如图，在△ABC中，AB=AC，∠B=40°，以B为圆心，BA的长为半径画弧，交BC于点D，连接AD，则∠DAC的度数是30°．
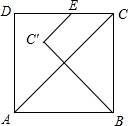如图所示，AB=4，AD=3，点E在CD上（不含端点C，D）的任一点，把△EBC沿BC折叠，当点C落在矩形ABCD的对角线上时，CE=$\frac{3}{2}$．
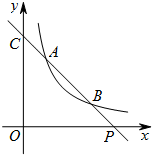如图，已知直线y=ax+b与双曲线$y=\frac{k}{x}$（x＞0）交于A（x1，y1），B（x2，y2）两点（A与B不重合），直线AB与x轴交于P（x0，0），与y轴交于点C．
6．若反比例函数y=$\frac{k}{x}$的图象过点（-3，1），则该图象还经过（ ）
| A． | （1，3） | B． | （3，-1） | C． | （3，1） | D． | （-1，-3） |