题目内容
2.用配方法解方程:(1)x2+5x-2=0.
(2)x2-$\frac{2}{3}$x-1=0.
分析 (1)把常数项-2移项后,应该在左右两边同时加上一次项系数5一半的平方,可得方程的解;
(2)把常数项-1移项后,应该在左右两边同时加上一次项系数-$\frac{2}{3}$的一半的平方,可得方程的解.
解答 解:(1)移项,得
x2+5x=2,
配方,得
(x+$\frac{5}{2}$)2=$\frac{33}{4}$,
开方,得
x+$\frac{5}{2}$=$±\frac{\sqrt{33}}{2}$,
x1=$\frac{-5+\sqrt{33}}{2}$,x2=$\frac{-5-\sqrt{33}}{2}$;
(2)移项,得
x2-$\frac{2}{3}$x=1,
配方,得
(x-$\frac{1}{3}$)2=$\frac{10}{9}$,
开方,得
x-$\frac{1}{3}$=$±\frac{\sqrt{10}}{3}$,
x1=$\frac{1+\sqrt{10}}{3}$,x2=$\frac{1-\sqrt{10}}{3}$.
点评 本题考查了配方法解一元二次方程,配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.下列事件中属于随机事件的是( )
| A. | 抛出的篮球会落下 | B. | 买2张双色球彩票,都中500万大奖 | ||
| C. | 25人中有3人是同月出生 | D. | 从装有黑球,白球的袋里摸出红球 |
11.下面说法中错误的是( )
| A. | 数轴上原点的位置是任意取的,不一定要居中 | |
| B. | 数轴上单位长度的大小要根据实际需要选取,1厘米长的线段可以代表1个单位长度,也可以代表2个、5个、10个、100个…单位长度,但一经取定,就不可改动 | |
| C. | 如果a<b,那么在数轴上表示a的点比表示b的点距离原点更近 | |
| D. | 所有的有理数都可以用数轴上的点表示,但不能说数轴上所有的点都表示有理数 |
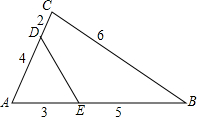 如图,△ABC中,AD=4,CD=2,AE=3,EB=5,BC=6,求DE的长.
如图,△ABC中,AD=4,CD=2,AE=3,EB=5,BC=6,求DE的长. 刘湘的爸爸是个工程师,专门搞机械零件研究发明,几年前自己开了家机械制造厂,自己设计,自己加工生产.有一天,他急需一个如图所示的配件,而这种配件又不能自己生产,附近厂家也没有能力生产,只能交代远在千里之外的一家大型工厂才能铸造生产.他在电话里努力地描述该配件的形状和大小,可对方一点儿也没弄明白,这可急坏了他.刘湘知道了此事,接过电话,很快将把这个零件的形状和尺寸告诉了对方,你认为刘湘是用的什么方法?
刘湘的爸爸是个工程师,专门搞机械零件研究发明,几年前自己开了家机械制造厂,自己设计,自己加工生产.有一天,他急需一个如图所示的配件,而这种配件又不能自己生产,附近厂家也没有能力生产,只能交代远在千里之外的一家大型工厂才能铸造生产.他在电话里努力地描述该配件的形状和大小,可对方一点儿也没弄明白,这可急坏了他.刘湘知道了此事,接过电话,很快将把这个零件的形状和尺寸告诉了对方,你认为刘湘是用的什么方法? 如图所示,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,则∠B的度数为52.
如图所示,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,则∠B的度数为52.