题目内容
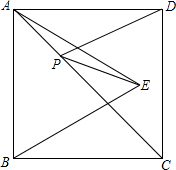 如图,正方形ABCD的边长为1+
如图,正方形ABCD的边长为1+| 3 |
考点:轴对称-最短路线问题
专题:
分析:由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,△ABE是等边三角形,得出∠ABE=60°,进而得出∠FBC=30°,解直角三角形求得CF=
BC=
(1+
)=
+1,然后根据平行线分线段成比例定理求得
=
,进一步得出P′G=
,从而求得点P到AB的距离为
.
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| AP′ |
| AC |
| ||
|
| 3 |
| 3 |
解答: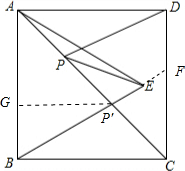 解:设BE与AC交于点P′,连接BD.
解:设BE与AC交于点P′,连接BD.
∵点B与D关于AC对称,
∴P′D=P′B,
∴P′D+P′E=P′B+P′E=BE最小.
∵AB=1+
,
又∵△ABE是等边三角形,
∴BE=AB=1+
.
延长BE交DC于F,作P′G⊥AB于G,
∵△ABE是等边三角形,
∴∠ABE=60°,
∴∠FBC=30°,
∴CF=
BC=
(1+
)=
+1,
∵AB∥CD,
∴
=
=
,
∴
=
,
∴
=
,
∵P′G∥BC,
∴
=
,
即
=
,
∴P′G=
,
∴点P到AB的距离为
,
故答案为
.
 解:设BE与AC交于点P′,连接BD.
解:设BE与AC交于点P′,连接BD.∵点B与D关于AC对称,
∴P′D=P′B,
∴P′D+P′E=P′B+P′E=BE最小.
∵AB=1+
| 3 |
又∵△ABE是等边三角形,
∴BE=AB=1+
| 3 |
延长BE交DC于F,作P′G⊥AB于G,
∵△ABE是等边三角形,
∴∠ABE=60°,
∴∠FBC=30°,
∴CF=
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
∵AB∥CD,
∴
| CF |
| AB |
| CP′ |
| AP′ |
| ||
| 3 |
∴
| AP′ |
| CP′ |
| 3 |
∴
| AP′ |
| AC |
| ||
|
∵P′G∥BC,
∴
| P′G |
| BC |
| AP′ |
| AC |
即
| P′G | ||
|
| ||
|
∴P′G=
| 3 |
∴点P到AB的距离为
| 3 |
故答案为
| 3 |
点评:本题考查的是轴对称-最短路线问题,等边三角形的性质,正方形的性质,平行线分线段成比例定理,解直角三角形等,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你的0.85m给我,我就有10颗”.如果设小刚的弹珠数为1.1m颗,小龙的弹珠数为0.5m颗,则列出的方程组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 要在河边CD修建一个水泵站,分别向张村A、李庄B送水.已知张村,李庄到河边的距离分别是480米和270米,两村之间AB距离为960米,求送水管最少要用多少米.
要在河边CD修建一个水泵站,分别向张村A、李庄B送水.已知张村,李庄到河边的距离分别是480米和270米,两村之间AB距离为960米,求送水管最少要用多少米. 如图,直线AB,CD,EF相交于点O,EF⊥AB,OG为∠COF的平分线,若∠BOC:∠COG=5:1,求∠DOF的度数.
如图,直线AB,CD,EF相交于点O,EF⊥AB,OG为∠COF的平分线,若∠BOC:∠COG=5:1,求∠DOF的度数.