题目内容
18.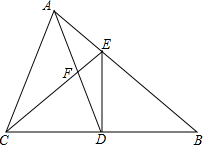 已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)求证:△ABC∽△FCD;
(2)若△FCD的面积为7.5,BC=10,求DE的长.
分析 (1)先由线段垂直平分线的性质证明CE=BE,从而得到∠DCF=∠CBA,由AD=AC可知∠CDF=∠BCA,从而得到△ABC∽△FCD;
(2)由相似三角形的面积等于相似比的平方可求得△ABC的面积为30,从而可求得AH=6,过A作AH⊥CB于H.由等腰三角形的性质可知HC=DH=$\frac{1}{4}$BC,然后证明△BDE∽△BHA,利用相似三角形的性质可求得DE的长.
解答 (1)证明:∵D是BC边上的中点,DE⊥BC
∴CE=BE
∴∠DCF=∠CBA.
∵AC=AD,
∴∠CDF=∠BCA.
∴△ABC∽△FCD.
(2)解:过A作AH⊥CB于H.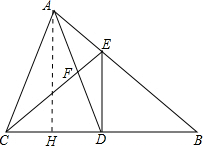
∵AC=AD,AH⊥CD,
∴CH=DH=$\frac{1}{2}CD=\frac{1}{4}BC$=2.5.
∵△ABC∽△FCD,
∴$\frac{{S}_{△ABC}}{{S}_{△FCD}}=(\frac{BC}{CD})^{2}=4$.
∴S△ABC=4S△FCD=30.
∴AH=$\frac{2{S}_{△ABC}}{BC}$=6.
∵AH⊥CB,ED⊥CB
∴AH∥ED
∴$\frac{DE}{AH}=\frac{BD}{BH}$.
∴DE=$\frac{AH•BD}{BH}$=$\frac{6×5}{5+2.5}$=4.
点评 本题主要考查的是相似三角形的性质和判定、利用相似三角形的性质求得△ABC的面积是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
9.已知等腰△ABC中,∠A=50°,则∠B的度数为( )
| A. | 65° | B. | 80° | C. | 50°或80° | D. | 50°或80°或65° |
6.二元一次方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解为$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,则一次函数y=5-x与y=2x-1的交点坐标为( )
| A. | (2,3) | B. | (3,2) | C. | (-2,3) | D. | (2,-3) |
7.下列计算正确的是( )
| A. | x3+x2=x5 | B. | x6÷x3=x2 | C. | x3•x2=x5 | D. | (x3)2=x5 |
