题目内容
7.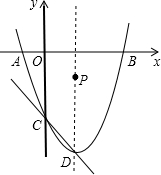 如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为D,问:在抛物线的对称轴上是否存在一点P,使得以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,求出点P 的坐标;若不存在,说明理由.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为D,问:在抛物线的对称轴上是否存在一点P,使得以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,求出点P 的坐标;若不存在,说明理由.
分析 先通过解方程x2-2x-3=0得到A(-1,0),B(3,0),再求自变量为0时的函数值得到C(0,-3),接着把解析式配成顶点式得到D(1,-4),抛物线的对称轴为直线x=1,作PH⊥CD于H,CE⊥直线x=1于E,如图,易得△CDE为等腰直角三角形,则∠CDE=45°,再判断△PHD为等腰直角三角形得到PH=$\frac{\sqrt{2}}{2}$PD,根据切线的判定方法,当PA=PB=PH时,以P为圆心的圆经过A、B两点,并且与直线CD相切,设此时P点坐标为(1,m),则PD=m+4,则PH2=$\frac{1}{2}$(m+4)2,而PA2=(1+1)2+m2,于是得到$\frac{1}{2}$(m+4)2=(1+1)2+m2,然后解方程求出m的值即可得到满足条件的P点坐标.
解答 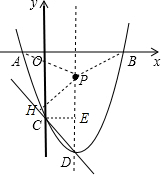 解:存在.
解:存在.
当y=0时,x2-2x-3=0,解得x1=-1,x2=-3,则A(-1,0),B(3,0),
当x=0时,y=x2-2x-3=-3,则C(0,-3),
y=x2-2x-3=(x-1)2-4,则D(1,-4),抛物线的对称轴为直线x=1,
作PH⊥CD于H,CE⊥直线x=1于E,如图,
∵CE=1,DE=-3-(-4)=1,
∴△CDE为等腰直角三角形,
∴∠CDE=45°,
∴△PHD为等腰直角三角形,
当PA=PB=PH时,以P为圆心的圆经过A、B两点,并且与直线CD相切,
设此时P点坐标为(1,m),则PD=m+4,
∵PH=$\frac{\sqrt{2}}{2}$PD,
∴PH2=$\frac{1}{2}$(m+4)2,
而PA2=(1+1)2+m2,
∴$\frac{1}{2}$(m+4)2=(1+1)2+m2,
∴m=4-2$\sqrt{6}$或m=4+2$\sqrt{6}$(舍去),
∴满足条件的P点坐标为(1,4-2$\sqrt{6}$).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了切线的判定和等腰三角形的性质.

| A. | 106×106 | B. | 1.06×106 | C. | 1.06×108 | D. | 1.06×109 |
| A. |  禁止驶入 | B. |  禁止行人通行 | ||
| C. |  禁止长时间停放 | D. |  禁止临时或长时间停放 |
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
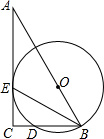 如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.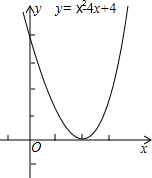 (1)抛物线与x轴有1个交点,它们的横坐标是2;
(1)抛物线与x轴有1个交点,它们的横坐标是2;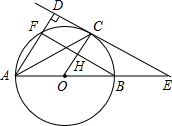 如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.
如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.