题目内容
13.解方程组:$\left\{\begin{array}{l}{2x-3y+4z=11}\\{3x+y-2z=3}\\{z=x+y}\end{array}\right.$.分析 用消元的思想,转化为二元一次方程组,再转化为一元一次方程,再解方程即可.
解答 解:$\left\{\begin{array}{l}{2x-3y+4z=11①}\\{3x+y-2z=3②}\\{z=x+y③}\end{array}\right.$,
将③代入①②得,$\left\{\begin{array}{l}{6x+y=11④}\\{x-y=3⑤}\end{array}\right.$,
④+⑤得,7x=14,
解得x=2,
把x=2代入⑤,得y=-1,
把x=2,y=-1代入③得,z=1,
故不等式组的解集为$\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$.
点评 本题考查了三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解二元一次方程组较简单.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
18.下列计算正确的是( )
| A. | (-2)×(-3)=-6 | B. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | C. | 2×0=0 | D. | $\sqrt{1}=±1$ |
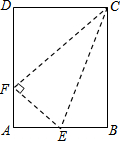 如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.
如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.