题目内容
如图,两块三角板,其中∠B=∠E=90°,∠C=30°,∠FDE=45°,AB=DE= .先将两块三角板叠合在一起,使边DE与AB重合(如图①),再将△DEF沿AB所在直线向左平移,使点F落在AC上(如图②),求平移距离BE的长.
.先将两块三角板叠合在一起,使边DE与AB重合(如图①),再将△DEF沿AB所在直线向左平移,使点F落在AC上(如图②),求平移距离BE的长.

解:∵∠B=∠E=90°,∠C=30°,∠FDE=45°,AB=DE= .
.
∴AF= ,
,
在图②中,∴∠FAE=60°,
∴勾股定理得,AE2=(2AE)2-( )2,
)2,
解得,AE=1,
∴BE=AB-AE= -1.
-1.
故答案为: -1.
-1.
分析:先由图①,根据勾股定理求出AF,再在图②中,由∠C=30°,∠FAE=60°,再得出∠AFE=30°,由勾股定理得出AE,从而求得平移距离AD或BE.
点评:本题考查了相似三角形的判定和性质,解直角三角形,是基础知识要熟练掌握.
 .
.∴AF=
 ,
,在图②中,∴∠FAE=60°,
∴勾股定理得,AE2=(2AE)2-(
 )2,
)2,解得,AE=1,
∴BE=AB-AE=
 -1.
-1.故答案为:
 -1.
-1.分析:先由图①,根据勾股定理求出AF,再在图②中,由∠C=30°,∠FAE=60°,再得出∠AFE=30°,由勾股定理得出AE,从而求得平移距离AD或BE.
点评:本题考查了相似三角形的判定和性质,解直角三角形,是基础知识要熟练掌握.

练习册系列答案
相关题目
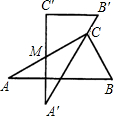 如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是
如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是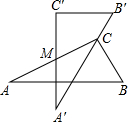 (2011•太原二模)如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于
(2011•太原二模)如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于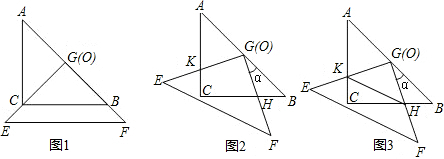
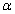 满足0<º
满足0<º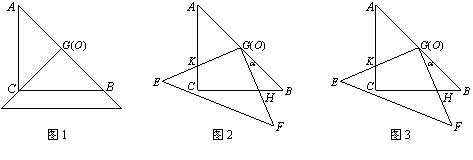
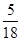 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由. 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于________.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=2,则这块直角三角板顶点A、A′之间的距离等于________.