题目内容
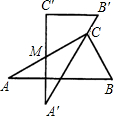 如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是
如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是分析:此题先连接CC′,根据M是AC、AC′的中点,AC=A′C′,得出CM=A′M=C′M=
AC=5,再根据∠A′=∠A′CM=30°,得出∠CMC′=60°,△MCC′为等边三角形,从而证出C′C=CM,即可得出答案.
| 1 |
| 2 |
解答: 解:连接C′C,∵两块三角板重叠在一起,较长直角边的中点为M,
解:连接C′C,∵两块三角板重叠在一起,较长直角边的中点为M,
∴M是AC、AC′的中点,AC=A′C′,
∴CM=A′M=C′M=
AC=5,
∴∠A′=∠A′CM=30°,
∴∠CMC′=60°,
∴△MCC′为等边三角形,
∴C′C=CM=5,
∴C′C长为5.
故填:5.
 解:连接C′C,∵两块三角板重叠在一起,较长直角边的中点为M,
解:连接C′C,∵两块三角板重叠在一起,较长直角边的中点为M,∴M是AC、AC′的中点,AC=A′C′,
∴CM=A′M=C′M=
| 1 |
| 2 |
∴∠A′=∠A′CM=30°,
∴∠CMC′=60°,
∴△MCC′为等边三角形,
∴C′C=CM=5,
∴C′C长为5.
故填:5.
点评:本题考查了旋转的性质,要与特殊三角形的性质与判定相结合.

练习册系列答案
相关题目
 角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A
角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A 30°,AC
30°,AC
 如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是________.
如图,是两块完全一样的含30°角的三角板,分别记作△ABC与△A′B′C′,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A′B′C′的斜边A′B′上,当∠A=30°,AC=10时,则此时两直角顶点C、C′间的距离是________.
