Question

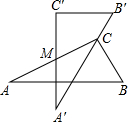（2011•太原二模）如图是两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C．已知AC=2，则这块直角三角板顶点A、A′之间的距离等于

1

．

Answer 1

分析：连接AA′，先由点M是线段AC、线段A′C′的中点可知，AM=MC=A′M=MC′=1，故可得出∠MCA′=∠MA′C=30°，故可得出∠MCB′的度数，根据四边形内角和定理可得出∠C′MC的度数，进而可判断出△AA′M的形状，进而得出结论．

解答：解：连接AA′，
∵点M是线段AC、线段A′C′的中点，AC=2，
∴AM=MC=A′M=MC′=1，
∵∠MA′C=30°，
∴∠MCA′=∠MA′C=30°，
∴∠MCB′=180°-30°=150°，
∴∠C′MC=360°-（∠MCB′+∠B′+∠C′）=180°-（150°+60°+90°）=60°，
∴∠AMA′=∠C′MC=60°，
∴△AA′M是等边三角形，
∴AA′=AM=1．
故答案为：1．

点评：本题考查的是等边三角形的判定与性质，根据题意作出辅助线，构造出等边三角形是解答此题的关键．