证明任意四个连续整数之和不可能是384．题目和参考答案——青夏教育精英家教网—

题目内容

20．证明任意四个连续整数之和不可能是384．

分析首先假设任意四个连续整数之和是384，进而表示出各数，再求出x的值，进而得出答案．

解答证明：假设任意四个连续整数之和是384，
第一个整数为：x，则其余整数分别为：x+1，x+2，x+3，
故x+x+1+x+2+x+3=384，
解得：x=94.5，
这与x为整数互相矛盾，故假设不成立，
原命题正确，即任意四个连续整数之和不可能是384．

点评此题主要考查了反证法，正确把握反证法的步骤是解题关键．

练习册系列答案

相关题目

10．

数a，b在数轴上的位置如图所示，下列各式正确的是（　　）

11．若“ω”是新规定的某种运算符号，设aωb=3a-2b，
（1）计算：（x²+y）ω（x²-y）
（2）若x=-2，y=2，求出（x²+y）ω（x²-y）的值．

8．已知：x=-1，y=$\frac{1}{2}$，求x²-4xy+4y²的值，则正确的是（　　）

15．

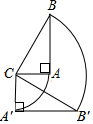如图所示，将直角△ABC向下旋转90°，已知BC=5厘米，AB=4厘米，AC=3厘米，求△ABC扫过的面积．

5．若二次函数y=a（x-m）²的图象经过点（1，1）且关于直线x=$\frac{1}{2}$对称，求这个二次函数的解析式．

12．用加减消元法解方程组：$\left\{\begin{array}{l}{3x+2y=7，①}\\{x+2y=-3．②}\end{array}\right.$．（1）①-②，得2x=4；（2）所以x=2；（3）把x=2代入①，得y=$\frac{1}{2}$；（4）所以这个方程组得解为$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$最先出现错误的一步是（　　）

9．已知函数y=mx²的图象经过点（-5，1），则函数的解析式为y=$\frac{1}{25}$x²．

16．

如图，A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出它们的中点M、N．若测得MN=10m，则A、B两点的距离为20m．

试题分类