题目内容
把半径为1的圆放在边长为9、12、15的三角形内任意移动,求在该三角形内,这张圆形纸片不能接触到部分的面积.
考点:直线与圆的位置关系
专题:计算题
分析:如图,根据勾股定理的逆定理可证明△ACB为直角三角形,由于⊙D、⊙E和⊙F为半径为1的圆,且分别与△ABC的各边相切,根据切线的性质可得到DE∥AC,EF∥BC,DF∥AB,则△DEF∽△ABC,所以EF:DE:DF=3:4:5,设EF=3x,则DE=4x,DF=5x,所以GM=4x,NP=3x,HQ=5x,设AG=a,BP=b,根据切线长定理得AH=a,BQ=b,利用三角形三边的长得到
,解得
,然后根据扇形的面积公式和这张圆形纸片不能接触到部分的面积=S四边形AGDH-S扇形GDH+S正方形CNEM-S扇形MEN+S四边形BPFQ-S扇形PFQ进行计算.
|
|
解答:解:如图,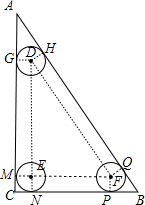 AC=12,BC=9,AB=15,
AC=12,BC=9,AB=15,
∵92+122=152,
∴BC2+AC2=AB2,
∴△ACB为直角三角形,
⊙D、⊙E和⊙F为半径为1的圆,且分别与△ABC的各边相切,如图,
∴DE∥AC,EF∥BC,DF∥AB,
∴△DEF∽△ABC,
∴EF:DE:DF=9:12:15=3:4:5,
设EF=3x,则DE=4x,DF=5x,
∴GM=4x,NP=3x,HQ=5x,
设AG=a,BP=b,则AH=a,BQ=b,
∴
,解得
,
∴这张圆形纸片不能接触到部分的面积=S四边形AGDH-S扇形GDH+S正方形CNEM-S扇形MEN+S四边形BPFQ-S扇形PFQ
=S四边形AGDH+S正方形CNEM+S四边形BPFQ-(S扇形GDH+S扇形MEN+S扇形PFQ)
=S四边形AGDH+S正方形CNEM+S四边形BPFQ-S⊙D
=2×
×3×1+1×1+2×
×2×1-π•12
=6-π.
 AC=12,BC=9,AB=15,
AC=12,BC=9,AB=15,∵92+122=152,
∴BC2+AC2=AB2,
∴△ACB为直角三角形,
⊙D、⊙E和⊙F为半径为1的圆,且分别与△ABC的各边相切,如图,
∴DE∥AC,EF∥BC,DF∥AB,
∴△DEF∽△ABC,
∴EF:DE:DF=9:12:15=3:4:5,
设EF=3x,则DE=4x,DF=5x,
∴GM=4x,NP=3x,HQ=5x,
设AG=a,BP=b,则AH=a,BQ=b,
∴
|
|
∴这张圆形纸片不能接触到部分的面积=S四边形AGDH-S扇形GDH+S正方形CNEM-S扇形MEN+S四边形BPFQ-S扇形PFQ
=S四边形AGDH+S正方形CNEM+S四边形BPFQ-(S扇形GDH+S扇形MEN+S扇形PFQ)
=S四边形AGDH+S正方形CNEM+S四边形BPFQ-S⊙D
=2×
| 1 |
| 2 |
| 1 |
| 2 |
=6-π.
点评:本题考查了线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了相似三角形的判定与性质、勾股定理的逆定理和扇形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于x的一元二次方程x2+x-1=0的两个根分别为a,b,则
+
=( )
| 1 |
| a |
| 1 |
| b |
| A、2 | B、1 | C、-1 | D、-2 |
 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.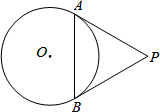 如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是
如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是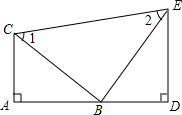 已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.
已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.