Question

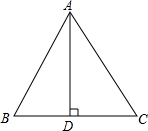如图，等边△ABC的边长为6

3

cm，AD是高，若以点D为圆心，r为半径作圆，试分别确定⊙D与AB有怎样的位置关系？
（1）r=3cm；
（2）r=4.5cm；
（3）r=6cm．

Answer 1

考点：直线与圆的位置关系

专题：

分析：首先过点D作DE⊥AB于点E，进而求出DE的长，进而利用直线与圆的位置关系得出答案．

解答：解：过点D作DE⊥AB于点E，
∵等边△ABC的边长为6

3

cm，AD是高，
∴AD=ABsin60°=9cm，∠BAD=30°，
∴DE=4.5cm，
故当（1）r=3cm时，⊙D与AB相离，
（2）r=4.5cm时，⊙D与AB相切；
（3）r=6cm时，⊙D与AB相交．

点评：此题主要考查了直线与圆的位置关系判断，正确求出DE的长是解题关键．