题目内容
已知:抛物线y=-x2-2x+3与x轴相交于A、B两点(点A在点B左侧),与y轴交于C,顶点为P.已知点M是抛物线上的一个动点,且在第二象限内,当△ACM的面积最大时,求出此时点M的坐标和△ACM的最大面积.
考点:抛物线与x轴的交点
专题:
分析:由函数的解析式画出大致图象,当-2<x<0或-3<x≤-2时,如图1、2,设△ACM的面积为S,M(x,-x2-2x+3)(x<0),作ME⊥y轴,就有ME=-x,OE=-x2-2x+3,由三角形的面积公式和梯形的面积公式就可以求出结论.
解答:解:设△ACM的面积为S,M(x,-x2-2x+3)(x<0),作ME⊥y轴,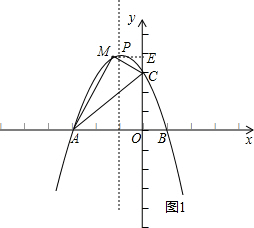
∴ME=-x,OE=-x2-2x+3.
∵y=-x2-2x+3,
∴y=0时,0=-x2-2x+3,
∴x1=1,x2=-3.
∵点A在点B左侧,
∴OA=3.
如图1,当-2<x<0时,
S1=
-
-4.5,
=-
x2-
x,
=-
(x+
)2+
,
∴a=-
<0,抛物线开口向下,函数有最大值.
∴x=-
时,S最大=
;
∵-2<x<0,
x=-2时,S最大=3
如图2,当-3<x≤-2时,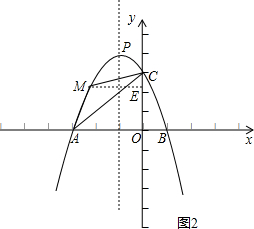
S2=
+
-
,
=-
x2-
x,
=-
(x+
)2+
,
∴a=-
<0,
∴抛物线的开口向下,在对称轴的左侧S随x的增大而增大.
∴x=-2时,S最大=3
∵
>3,
∴x=-
时,S△ACM最大=
.
∴M(-
,
).
答:M(-
,
)时,S△ACM最大=
.

∴ME=-x,OE=-x2-2x+3.
∵y=-x2-2x+3,
∴y=0时,0=-x2-2x+3,
∴x1=1,x2=-3.
∵点A在点B左侧,
∴OA=3.
如图1,当-2<x<0时,
S1=
| (-x+3)(-x2-2x+3) |
| 2 |
| (-x2-2x+3-3)(-x) |
| 2 |
=-
| 3 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴a=-
| 3 |
| 2 |
∴x=-
| 3 |
| 2 |
| 27 |
| 8 |
∵-2<x<0,
x=-2时,S最大=3
如图2,当-3<x≤-2时,

S2=
| (-x+3)(-x2-2x+3) |
| 2 |
| -x(3+x2+2x-3) |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴a=-
| 3 |
| 2 |
∴抛物线的开口向下,在对称轴的左侧S随x的增大而增大.
∴x=-2时,S最大=3
∵
| 27 |
| 8 |
∴x=-
| 3 |
| 2 |
| 27 |
| 8 |
∴M(-
| 3 |
| 2 |
| 15 |
| 4 |
答:M(-
| 3 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |
点评:本题考查了二次函数的图象的性质的运用,三角形的面积公式的运用,梯形的面积公式的运用,抛物线与x轴的交点坐标的运用,分类讨论的运用.解答时求出S与x的关系式是关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a3-a2=a |
| B、a6÷a2=a3 |
| C、(a-b)2=a2-b2 |
| D、(-3a)3=-27a3 |
下列各对数中,数值相等的是( )
| A、32与23 | ||||
| B、-32与(-3)2 | ||||
| C、-23与(-2)3 | ||||
D、(
|
 如图,等边△ABC的边长为6
如图,等边△ABC的边长为6