题目内容
如图，上下底面为全等的正六边形礼盒，其中礼盒高10cm，上下底面正六边形的边长为12cm，若用彩带按如图所示的方式包扎礼盒，则所需彩带的长度至少为考点：正多边形和圆
专题：
分析：先利用正六边形的性质求得底面对边之间的距离，然后所有棱长相加即可．
解答：
解根据题意，作出实际图形的上底，如图，AC，CD是上底面的两边．作CB⊥AD于点B，
∵∠ACD=120°，AC=12cm，
∴∠ACB=
×120°=60°，
∴AB=AC•sin60°=12×
=6
cm，
∴AD=12
cm，
∵礼盒高10cm，
∴彩带的长至少=12
×6+10×6=（72
+60）cm．
故答案为：（72
+60）cm．
解根据题意，作出实际图形的上底，如图，AC，CD是上底面的两边．作CB⊥AD于点B，∵∠ACD=120°，AC=12cm，
∴∠ACB=
| 1 |
| 2 |
∴AB=AC•sin60°=12×
| ||
| 2 |
| 3 |
∴AD=12
| 3 |
∵礼盒高10cm，
∴彩带的长至少=12
| 3 |
| 3 |
故答案为：（72
| 3 |
点评：本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
练习册系列答案
相关题目
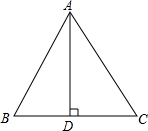如图，等边△ABC的边长为6