题目内容
19.化简:(1)x(1-x)-(x+2)(2-x)+(2x2-x)÷x
(2)$\frac{x}{3-x}$-$\frac{{x}^{2}+8x+16}{{x}^{2}+3x}$÷($\frac{-2}{x+3}$+$\frac{4}{x}$-1).
分析 (1)原式利用单项式乘多项式,平方差公式,以及多项式除以单项式法则计算,即可得到结果;
(2)原式括号中通分并利用同分母分式的加减法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=x-x2-4+x2+2x-1=3x-5;
(2)原式=$\frac{x}{3-x}$-$\frac{(x+4)^{2}}{x(x+3)}$÷$\frac{-2x+4x+12-{x}^{2}-3x}{x(x+3)}$=-$\frac{x}{x-3}$-$\frac{(x+4)^{2}}{x(x+3)}$•$\frac{x(x+3)}{-(x+4)(x-3)}$=-$\frac{x}{x-3}$+$\frac{x+4}{x-3}$=$\frac{4}{x-3}$.
点评 此题考查了分式的混合运算,单项式乘以多项式,平方差公式,以及整式的除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
7. 如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
 如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )| A. | 12° | B. | 15° | C. | 30° | D. | 10° |
14.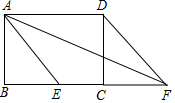 如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
 如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )
如图,矩形ABCD中,点E是BC边上一点,连接AE,将△ABE向右平移得到△DCF,连接AF.若四边形AEFD为菱形,AF=4$\sqrt{5}$,BE:EC=3:2,则AD长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | 5 | D. | $2\sqrt{5}$ |
11.若甲、乙、丙、丁四位射击运动员10次射击训练的平均成绩均为9.1环,方差分别为S甲2=0.80,S乙2=1.31,S丙2=1.72,S丁2=0.42,则成绩最稳定的运动员是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
8.在下列关于x的函数中,一定是二次函数的是( )
| A. | y=x2 | B. | y=ax2+bx+c | C. | y=8x | D. | y=x2(1+x) |

 在Rt△ABC中,∠A=90°.
在Rt△ABC中,∠A=90°.