题目内容
 如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论正确的是
如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论正确的是①P在∠A的平分线上;②QP∥AR;③△BRP≌△QSP.
考点:等边三角形的性质
专题:
分析:首先根据角平分线上点的性质,推出①正确,再根据AQ=PQ,推出相关角相等,通过等量代换即可得∠QPA=∠QAR,即可推出②正确,依据等边三角形的性质和外角的性质推出∠PQS=∠B,便可推出结论③.
解答:解:∵PR=PS,PR⊥AB,PS⊥AC,
∴P在∠A的平分线上,故①正确;
∵AQ=PQ,
∴∠PAR=∠QPA,
∵P在∠A的平分线上,
∴∠PAR=∠QPA,
∴∠QPA=∠PAR
∴QP∥AR,故②正确;
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∴∠PAR=∠QPA=30°,
∴∠PQS=60°,
在△BRP和△QSP中,
∵
,
∴△BRP≌△QSP(AAS),
∴①②③都正确,
故答案为:①②③.
∴P在∠A的平分线上,故①正确;
∵AQ=PQ,
∴∠PAR=∠QPA,
∵P在∠A的平分线上,
∴∠PAR=∠QPA,
∴∠QPA=∠PAR
∴QP∥AR,故②正确;
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∴∠PAR=∠QPA=30°,
∴∠PQS=60°,
在△BRP和△QSP中,
∵
|
∴△BRP≌△QSP(AAS),
∴①②③都正确,
故答案为:①②③.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质、等边对等角,直角三角形的性质,平行线的判定,关键在于熟练运用等边三角形的性质、全等三角形的判定定理,认真推理计算相关的等量关系.

练习册系列答案
相关题目
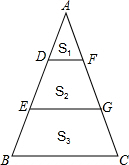 如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )
如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:3:6 |
用长4米的铝材制成一个矩形窗框,使它的面积为0.75米2.若设它的一边长为x米,根据题意列出关于x的方程为( )
| A、x(2-x)=0.75 |
| B、2x(2-x)=0.75 |
| C、x(4-2x)=0.75 |
| D、x(4-x)=0.75 |
下列四组线段中可以构成直角三角形的是( )
| A、3,4,5 |
| B、4,5,6 |
| C、2,3,4 |
| D、7,24,26 |
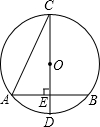 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件:
如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件: 已知:如图,AD=BC,AC=BD.
已知:如图,AD=BC,AC=BD.