题目内容
已知A、B、C三点在同一直线上,AB=12cm,BC=4cm,P、Q分别是AB、AC的中点,求PQ的长.
考点:两点间的距离
专题:
分析:分类讨论:C在线段AB上,C在线段AB的延长线上,根据线段的和差,可得AC的长,根据线段中点的性质,可得AP,AQ的长,再根据线段的和差,可得答案.
解答:解:当C在线段AB上时,由线段的和差,得AC=AB-BC=12-4=8cm,
由P、Q分别是AB、AC的中点,得
AP=0.5AB=6cm,AQ=0.5AC=4cm,
由线段的和差,得
PQ=AP-AQ=6-4=2cm;
当C在线段AB的延长线上时,由线段的和差,得AC=AB+BC=12+4=16cm,
由P、Q分别是AB、AC的中点,得
AP=0.5AB=6cm,AQ=0.5AC=8cm,
由线段的和差,得
PQ=AQ-AP=8-6=2cm.
由P、Q分别是AB、AC的中点,得
AP=0.5AB=6cm,AQ=0.5AC=4cm,
由线段的和差,得
PQ=AP-AQ=6-4=2cm;
当C在线段AB的延长线上时,由线段的和差,得AC=AB+BC=12+4=16cm,
由P、Q分别是AB、AC的中点,得
AP=0.5AB=6cm,AQ=0.5AC=8cm,
由线段的和差,得
PQ=AQ-AP=8-6=2cm.
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质,分类讨论是解题关键.

练习册系列答案
相关题目
已知二次函数y=ax2+bx+c的x、y的部分对应值如表:则该二次函数图象的对称轴为( )
| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| A、y轴 | ||
B、直线x=
| ||
| C、直线x=2 | ||
| D、直线x=2 |
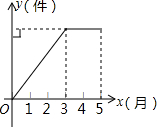 烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )
烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )| A、1月至3月每月生产总量逐月增加,4,5两月停止生产 |
| B、1月至3月每月生产总量不变,4,5两月均停止生产 |
| C、1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少 |
| D、1月至3月每月生产总量逐月增加,4,5两月生产量与3月持平 |
如果m的相反数是-1,则(-m)2014-(-m)2015的值是( )
| A、4029 | B、2 |
| C、0 | D、2015 |
 如图,已知l1∥l2,一块含45°角的直角三角板按如图所示放置,若∠1=35°,则∠2=( )
如图,已知l1∥l2,一块含45°角的直角三角板按如图所示放置,若∠1=35°,则∠2=( )| A、35° | B、30° |
| C、10° | D、5° |
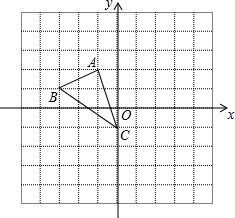 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1), 如图,M为⊙O内一点,利用尺规作一条弦AB,使AB过点M,且AM=BM.
如图,M为⊙O内一点,利用尺规作一条弦AB,使AB过点M,且AM=BM.