题目内容
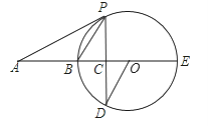
【题目】如图，BE是圆O的直径，A在EB的延长线上，AP为圆O的切线，P为切点，弦PD垂直于BE于点C．
（1）求证：∠AOD=∠APC；
（2）若OC：CB=1：2，AB=6，求圆O的半径及tan∠APB．
【答案】（1）见解析；（2）
【解析】试题分析：（1）连接OP，可结合已知的等角和等腰三角形、直角三角形的性质进行证明；
（2）根据OC、BC的比例关系，可用未知数表示出OC、BC的表达式，进而可得OP、OB的表达式；在Rt△AOP中，PC⊥OA，根据射影定理得：PC2=PCAC，PC2的表达式可在Rt△OPC中由勾股定理求得，由此求得未知数的知，从而确定PC、CE的长，也就能求出⊙O的半径和∠APB的正切值．
试题解析：（1）连接OP，
∵OP=OD，∴∠OPD=∠D，
∵PD⊥BE，
∴∠OCD=90°，
在Rt△OCD中，∠D+∠AOD=90°，
又∵AP是⊙O的切线，
∴AP⊥OP，
则∠OPD+∠APC=90°，
∴∠AOD=∠APC；
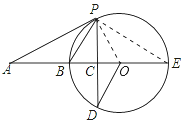
（2）连接PE，
∴∠BPE=90°（直径所对的圆周角是直角），
∵AP是⊙O的切线，
∴∠APB=∠OPE=∠PEA，
∵OC：CB=1：2，
∴设OC=x，则BC=2x，OP=OB=3x，
在Rt△OPC中，OP=3x，OC=x，由勾股定理得：
PC2=OP2﹣OC2=8x2，
在Rt△OPC中，PC⊥OA，由射影定理得：
PC2=OCAC，即8x2=x（2x+6），6x2=6x，
解得x=0（舍去），x=1，
∴OP=OB=3，PC=2
，CE=OC+OE=3+1=4，
∴tan∠APB=tan∠PEC=
，
∴⊙O的半径为3，∠APB的正切值是
．
【题目】甲、乙两个批发店销售同一种苹果，甲批发店的价格为每千克6元.在乙批发店，一次购买数量不超过
时，价格为每千克7元；一次购买数量超过时，其中有的价格为每千克7元，超过部分的价格为每千克5元，设小王在同个批发店一次购买苹果的数量为
.
（1）填表：
一次购买苹果的数量（单位： | 20 | 50 | 100 | … |
甲批发店花费（单位：元） | 300 | … | ||
乙批发店花费（单位：元） | 350 | … |
（2）分别用含
的代数式表示甲、乙批发店所花费的钱数.
（3）如果小王在同一个批发店一次购买苹果的数量为
，通过计算说明他在甲、乙两个批批发店所花费的钱数少？
