题目内容
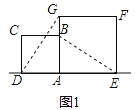
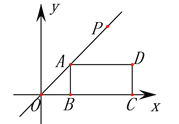
【题目】如图，在平面直角坐标系中，矩形ABCD的边BC在x轴的正半轴上，点B在点C的左侧，直线y=kx经过点A（2,2）和点P，且OP=4
，将直线y=kx沿y轴向下平移得到直线y=kx+b，若点P落在矩形ABCD的内部，则b的取值范围是（ ）
A. 0＜b＜2 B. －2＜b＜0 C. －4＜b＜2 D. －4＜b＜－2
【答案】D
【解析】解：如图作PE⊥AD于E交BC于F．∵直线y=kx经过点A（2，2），∴k=1，∴直线为y=x，设点P坐标（a，a）．∵OP=
，∴a2+a2=32，∴a2=16．∵a＞0，∴a=4，∴点P坐标（4，4），点E（4，2），点F（4，0），把点E（4，2），点F（4，0）分别代入y=x+b中，得到b=﹣2或﹣4，∴点P落在矩形ABCD的内部，∴﹣4＜b＜﹣2．故选D．
练习册系列答案
相关题目
【题目】某中学数学活动小组为了调查居民的用水情况，从某社区的
户家庭中随机抽取了
户家庭的月用水量，结果如下表所示：
月用水量（吨） |
|
|
|
|
|
|
|
户数 |
|
|
|
|
|
|
|
求这户家庭月用水量的平均数、众数和中位数；
根据上述数据，试估计该社区的月用水量；
由于我国水资源缺乏，许多城市常利用分段计费的方法引导人们节约用水，即规定每个家庭的月基本用水量为
（吨），家庭月用水量不超过（吨）的部分按原价收费，超过（吨）的部分加倍收费．你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适？简述理由．
