题目内容
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.

(1)探索发现
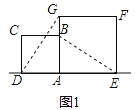
如图1,当点E在菱形ABCD内部时,连接CE,BP与CE的数量关系是_______,CE与AD的位置关系是_______.
(2)归纳证明
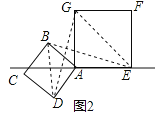
证明2,当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.
(3)拓展应用
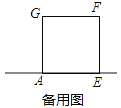
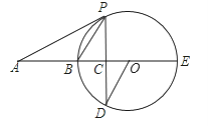
如图3,当点P在线段BD的延长线上时,连接BE,若AB=5,BE=13,请直接写出线段DP的长.
【答案】(1)BP=CE,CE⊥AD;(2)(1)中的结论仍成立.理由见解析; (3)PD= ![]() .
.
【解析】
(1)由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形,由等边△APE可得AP=AE,∠PAE=∠BAC=60°,减去公共角∠PAC得∠BAP=∠CAE,根据SAS可证得△BAP≌△CAE,故有BP=CE,∠ABP=∠ACE.由菱形对角线平分一组对角可证∠ABP=30°,故∠ACE=30°即CE平分∠ACD,由AC=CD等腰三角形三线合一可得CE⊥AD.
(2)证明过程同(1).
(3)由AB=5即△ABC为等边三角形可求得BD的长.连接CE,由(2)可求∠BCE=90°,故在Rt△BCE中,由勾股定理可求CE的长.又由(2)可得BP=CE,由DP=BP-BD即求得DP的长.
解:(1) ∵菱形ABCD中,∠ABC=60°
∴AB=BC=CD=AD,∠ADC=∠ABC=60°
∴△ABC、△ACD是等边三角形
∴AB=AC,AC=CD,∠BAC=∠ACD=60°
∵△APE是等边三角形
∴AP=AE,∠PAE=60°
∴∠BAC-∠PAC=∠PAE-∠PAC
即∠BAP=∠CAE
在△BAP与△CAE中
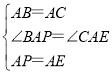
∴△BAP≌△CAE(SAS)
∴BP=CE,∠ABP=∠ACE
∵BD平分∠ABC
∴∠ACE=∠ABP=![]() ∠ABC=30°
∠ABC=30°
∴CE平分∠ACD
∴CE⊥AD
故答案为:BP=CE,CE⊥AD;
(2)(1)中的结论仍成立,证明如下:
设AD与CE交于点O
∵四边形ABCD为菱形,且∠ABC=60°
∴△ABC为等边三角形.
∴AB=AC,∠BAC=60°
∴∠BAP=∠CAE
又∵ΔAPE为等边三角形
∴AP=AE
在△BAP与△CAE中
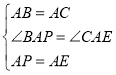
∴△BAP≌ΔCAE(SAS)
∴BP=CE
∴∠ACE=∠ABP=30°
又∵∠CAD=60°
∠A0C=90°
∴AD⊥CE;
(3) 连接CE,设AC与BD相交于点O
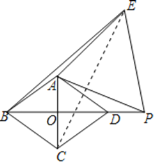
∵AB=5
∴BC=AC=AB=5
∴AO=![]() AC=
AC=![]()
∴BO=![]() =
=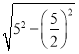 =
=![]()
∴BD=2BO=5![]()
∵∠BCE=∠BCA+∠ACE=90°,BE=13
∴CE=![]() =
=![]() =12
=12
由(2)可知,BP=CE=12
∴DP=BP-BD=12-5![]()
故答案为:(1)BP=CE,CE⊥AD;(2)(1)中的结论仍成立.理由见解析; (3)PD= ![]() .
.

【题目】如图,有个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
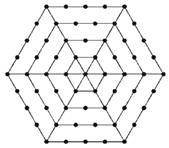
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | 6 |
该层对应的点数 | 1 | 6 | _____ | 18 | _____ | _____ |
(2)写出第n层所对应的点数为_____;
(3)如果某一层共96个点,那么它是第_____层,此时所有层中共有_____个点.