题目内容
 如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABCD的对称中心,正方形ABCD的边长为
如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABCD的对称中心,正方形ABCD的边长为| 10 |
| 2 |
(1)分别写出A,C,P三点的坐标;
(2)经过坐标原点O且顶点为P的抛物线是否经过C点,请说明理由?
(3)当t为何值时,△ANO与△DMR相似?
(4)设△HCR面积为S,求S与t的函数关系式;并求以A、B、C、R为顶点的四边形是梯形时t的值.
考点:二次函数综合题
专题:
分析:(1)过点D作DF⊥y轴于点F,作CE⊥x轴于点E,连接AC,由tan∠ABO=3可知OA:OB=3,设OA=3x,则OB=x,再根据正方形ABCD的边长为
利用勾股定理可求出OA及OB的长,由全等三角形的判定定理可得出△AOB≌△BEC≌△DFA,故可得出CD的坐标,利用中点坐标公式即可得出P点坐标;
(2)设经过坐标原点O且顶点为P的抛物线是y=a(x-h)2+k,由(1)可知C点的坐标,把其坐标代入抛物线的解析式检验即可;
(3)过点N作NE⊥AO,于点E,过点A作AF⊥MS于点F,MS⊥x轴于点S,求出M、N两点坐标,再分∠DRM=45°和∠MDR=45°两种情况进行讨论;
(4)由R速度为
,H速度为1,且∠ROH=45°,可知tan∠ROH=1,故RH始终垂直于x轴,RH=OH=t,设△HCR的边RH的高为h,h=|4-t|,再由三角形的面积公式即可得出结论;分情况进行讨论,顶边和底边分别为BC、AR,此时BC∥AR,结合已知和已证求出R点的坐标,求出t即可;顶边、底边分别为CR、AB,此时CR∥AB,结合已知和已证求出R点的坐标,求出t即可.
| 10 |
(2)设经过坐标原点O且顶点为P的抛物线是y=a(x-h)2+k,由(1)可知C点的坐标,把其坐标代入抛物线的解析式检验即可;
(3)过点N作NE⊥AO,于点E,过点A作AF⊥MS于点F,MS⊥x轴于点S,求出M、N两点坐标,再分∠DRM=45°和∠MDR=45°两种情况进行讨论;
(4)由R速度为
| 2 |
解答:解:(1)如图1,过点D作DF⊥y轴于点F,作CE⊥x轴于点E,连接AC,
∵tan∠ABO=3,
∴OA:OB=3,
∴设OA=3x,则OB=x,
∵正方形ABCD的边长为
,
∴△AOB中,OA2+OB2=AB2,即9x2+x2=(
)2,
解得x=1,
∴OA=3,OB=1,
∴A(0,3),
∵∠OAB+∠ABO=90°,∠ABO+∠CBE=90°,∠CBE+∠BCE=90°,
∴∠OAB=∠CBE,∠ABO=∠BCE,
在△AOB与△BEC中,
,
∴△AOB≌△BEC(SAS),
同理可得,△AOB≌△BEC≌△DFA,
∴BE=DE=3,CE=AF=1,
∴C(4,1),D(3,4),
∵P为正方形ABCD的对称中心,
∴P是AC的中点,
∴P(
,
),即(2,2),
故A(0,3),C(4,1)P(2,2);
(2)经过坐标原点O且顶点为P的抛物线不过C点,
理由如下:
设经过坐标原点O且顶点为P的抛物线是y=a(x-h)2+k,
∵P(2,2),
∴y=a(x-2)2+2,
∴0=a(0-2)2+2,
解得:a=-
,
∴y=-
(x-2)2+2,
∵C(4,1),
∴当x=4时,y=0≠1,
∴经过坐标原点O且顶点为P的抛物线不经过C点;
(3)
如图2,过点N作NE⊥AO于点E,过点A作AF⊥MS于点F,MS⊥x轴于点S,
由(1)可得:B(1,0),
∴直线AB的解析式为:y=-3x+3①;
直线OP的解析式为:y=x②,
①②联立得
,
解得
,
直线CD的解析式是:y=-3x+13,
解方程组:
,
解得
得:则M的坐标是:(
,
),
∴ON=
,OM=
,
∵AD2+DM2=AF2+MF2,即10+MD2=(
)2+(
)2,
∴DM=
,AN=
,
当∠MDR=45°时,
∵∠AON=45°,
∴∠MDR=∠AON,
∵AN∥DM,
∴∠ANO=∠DMP,
∴△ANO与△DMR相似,则△ANO∽△RMD,
∴
=
,即
=
,解得MR=
,
则OR=OM-MR=2
,
故t=2,
同理可得:当∠DRM=45°时,t=3,△ANO与△DMR相似,
综上可知:t=2或3时当△ANO与△DMR相似;
(4)∵R速度为
,H速度为1,且∠ROH=45°,
∴tan∠ROH=1,
∴RH始终垂直于x轴,
∴RH=OH=t,
设△HCR的边RH的高为h,
∴h=|4-t|.
∴S△HCR=h•t•
=|-t2+4t|•
,
∴S=
-t2+2t(0<t<4)
或S=t2-2t(t>4);
故S=-
t2+2t(0<t≤4)或S=
t2-2t(t>4);
以A、B、C、R为顶点的梯形,有三种可能:
①顶边和底边分别为BC、AR,此时BC∥AR.如图3,延长AD,使其与OM相交于点R,
则AD的斜率=tan∠BAO=
则直线AD为:y=
+3.
则R坐标为(4.5,4.5),
则此时四边形ABCR为直角梯形,
则t=4.5;
②顶边、底边分别为CR、AB,此时CR∥AB,且R与M重合.
则CD的斜率=-3,且直线CD过点C,
则直线CD为:y-1=-3•(x-4),
则y=-3x+13,
∵OM与CD交于点M(即R),
∴M为(
,
)
∴此时四边形ABCR为梯形,
∴t=
,
③求AC,BR的解析式,进而求出R坐标(
,
)求出t=
.
综上所述,t=4.5或t=
或t=
.
∵tan∠ABO=3,

∴OA:OB=3,
∴设OA=3x,则OB=x,
∵正方形ABCD的边长为
| 10 |
∴△AOB中,OA2+OB2=AB2,即9x2+x2=(
| 10 |
解得x=1,
∴OA=3,OB=1,
∴A(0,3),
∵∠OAB+∠ABO=90°,∠ABO+∠CBE=90°,∠CBE+∠BCE=90°,
∴∠OAB=∠CBE,∠ABO=∠BCE,
在△AOB与△BEC中,
|
∴△AOB≌△BEC(SAS),
同理可得,△AOB≌△BEC≌△DFA,
∴BE=DE=3,CE=AF=1,
∴C(4,1),D(3,4),
∵P为正方形ABCD的对称中心,
∴P是AC的中点,
∴P(
| 0+4 |
| 2 |
| 3+1 |
| 2 |
故A(0,3),C(4,1)P(2,2);
(2)经过坐标原点O且顶点为P的抛物线不过C点,
理由如下:
设经过坐标原点O且顶点为P的抛物线是y=a(x-h)2+k,
∵P(2,2),
∴y=a(x-2)2+2,
∴0=a(0-2)2+2,
解得:a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
∵C(4,1),
∴当x=4时,y=0≠1,
∴经过坐标原点O且顶点为P的抛物线不经过C点;
(3)
如图2,过点N作NE⊥AO于点E,过点A作AF⊥MS于点F,MS⊥x轴于点S,

由(1)可得:B(1,0),
∴直线AB的解析式为:y=-3x+3①;
直线OP的解析式为:y=x②,
①②联立得
|
解得
|
直线CD的解析式是:y=-3x+13,
解方程组:
|
解得
|
得:则M的坐标是:(
| 13 |
| 4 |
| 13 |
| 4 |
∴ON=
3
| ||
| 4 |
13
| ||
| 4 |
∵AD2+DM2=AF2+MF2,即10+MD2=(
| 13 |
| 4 |
| 1 |
| 4 |
∴DM=
| ||
| 4 |
3
| ||
| 4 |
当∠MDR=45°时,
∵∠AON=45°,
∴∠MDR=∠AON,
∵AN∥DM,
∴∠ANO=∠DMP,
∴△ANO与△DMR相似,则△ANO∽△RMD,
∴
| MR |
| DM |
| AN |
| NO |
| MR | ||||
|
| ||||
|
5
| ||
| 4 |
则OR=OM-MR=2
| 2 |
故t=2,
同理可得:当∠DRM=45°时,t=3,△ANO与△DMR相似,
综上可知:t=2或3时当△ANO与△DMR相似;
(4)∵R速度为
| 10 |
∴tan∠ROH=1,
∴RH始终垂直于x轴,
∴RH=OH=t,
设△HCR的边RH的高为h,
∴h=|4-t|.
∴S△HCR=h•t•
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
或S=t2-2t(t>4);
故S=-
| 1 |
| 2 |
| 1 |
| 2 |
以A、B、C、R为顶点的梯形,有三种可能:
①顶边和底边分别为BC、AR,此时BC∥AR.如图3,延长AD,使其与OM相交于点R,
则AD的斜率=tan∠BAO=
| 1 |
| 3 |
则直线AD为:y=
| x |
| 3 |

则R坐标为(4.5,4.5),
则此时四边形ABCR为直角梯形,
则t=4.5;
②顶边、底边分别为CR、AB,此时CR∥AB,且R与M重合.
则CD的斜率=-3,且直线CD过点C,
则直线CD为:y-1=-3•(x-4),
则y=-3x+13,
∵OM与CD交于点M(即R),
∴M为(
| 13 |
| 4 |
| 13 |
| 4 |
∴此时四边形ABCR为梯形,
∴t=
| 13 |
| 4 |
③求AC,BR的解析式,进而求出R坐标(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
综上所述,t=4.5或t=
| 13 |
| 4 |
| 1 |
| 3 |
点评:本题考查相似三角形的判定和性质,涉及到全等三角形的判定和性质、二次函数的最值,正方形的性质及梯形的判定定理,解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知一个圆锥形零件的母线长为5,底面半径为2,则这个圆锥形零件的侧面积为( )
| A、5π | B、10π | C、3π | D、6π |
如图,它们是由一些火柴棒搭成的图案,按图①②③所示的规律依次下去,摆第2014个图案用火柴棒的根数是( )
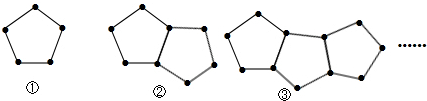

| A、4047 | B、8047 |
| C、4057 | D、8057 |



 如图,在平面直角坐标系中,点A的坐标为(2+
如图,在平面直角坐标系中,点A的坐标为(2+