题目内容
已知质数p、q使得表达式
及
都是自然数，试确定p2q的值．
| 2p+1 |
| q |
| 2q-3 |
| p |
先设p≥q，则有1≤
=2×
-
＜2，于是只能
=1，即p=2q-3，
而这时
=
=4-
，要使
为自然数，只能q=5，从而p=7，
再设p＜q，这时1≤
=2×
+
＜3，于是有下面两种情况：
①
=1，q=2p+1，此时
=
，
解得p=1，不合题意；
②
=2，2p+1=2q，左边为奇数，右边为偶数，矛盾．
故p2q=72×5=245．
故答案为：245．
| 2q-3 |
| p |
| q |
| p |
| 3 |
| p |
| 2q-3 |
| p |
而这时
| 2p+1 |
| q |
| 4q-5 |
| q |
| 5 |
| q |
| 2p+1 |
| q |
再设p＜q，这时1≤
| 2p+1 |
| q |
| p |
| q |
| 1 |
| q |
①
| 2p+1 |
| q |
| 2q-3 |
| p |
| 4p-1 |
| p |
解得p=1，不合题意；
②
| 2p+1 |
| q |
故p2q=72×5=245．
故答案为：245．
练习册系列答案
阅读快车系列答案
相关题目
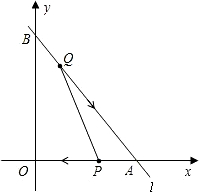线段AO上以每秒1个单位长度的速度向点O移动，设点Q，P移动的时间为t秒
