题目内容
如图,已知直线l的函数表达式为y=-| 4 | 3 |
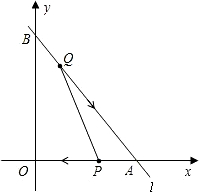 线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒(1)点A的坐标为
(2)当t=
(3)(2)中当△APQ与△AOB相似时,线段PQ所在直线的函数表达式为
分析:(1)根据一次函数图象上点的坐标特征,即与x轴的交点y=0,与y轴的交点x=0,求出A.B两点的坐标;
(2)当移动的时间为t时,根据△APQ∽△AOB,利用三角形的相似比求出t的值;
(3)当t=
秒时,PQ∥OB,PQ⊥OA,PA=
,即可求出P(
,0),进而求出线段PQ所在直线的函数表达式;
当t=
时PA=
,BQ=
,OP=
,有P(
,0),设Q点的坐标为(x,y),同上可求出Q的坐标,设PQ的表达式为y=kx+b,把P,Q两点的坐标分别为代入即可求出PQ的表达式.
(2)当移动的时间为t时,根据△APQ∽△AOB,利用三角形的相似比求出t的值;
(3)当t=
| 30 |
| 11 |
| 30 |
| 11 |
| 36 |
| 11 |
当t=
| 50 |
| 13 |
| 50 |
| 13 |
| 100 |
| 13 |
| 28 |
| 13 |
| 28 |
| 13 |
解答:解:(1)由y=-
x+8,
令x=0,得y=8;
令y=0,得x=6.
A,B的坐标分别是(6,0),(0,8);
(2)由BO=8,AO=6,根据勾股定理得AB=
=10.
当移动的时间为t时,AP=t,AQ=10-2t.
∵∠QAP=∠BAO,当
=
时,
△APQ∽△AOB,
=
,
∴t=
(秒).
∵∠QAP=∠BAO,
∴当
=
时,
△APQ∽△AOB,
∴
=
,
∴t=
(秒),
∴t=
秒或
秒,经检验,它们都符合题意,此时△AQP与△AOB相似;
(3)当t=
秒时,PQ∥OB,PQ⊥OA,PA=
,
∴OP=
,
∴P(
,0),
∴线段PQ所在直线的函数表达式为x=
,
当t=
时PA=
,BQ=
,OP=
,
∴P(
,0),
设Q点的坐标为(x,y),则有
=
,
∴
=
,
∴x=
,
当x=
时,y=-
×
+8=
,
∴Q的坐标为(
,
),
设PQ的表达式为y=kx+b,
则
,
∴
,
∴PQ的表达式为y=
x-
.
| 4 |
| 3 |
令x=0,得y=8;
令y=0,得x=6.
A,B的坐标分别是(6,0),(0,8);
(2)由BO=8,AO=6,根据勾股定理得AB=
| BO2+AO2 |
当移动的时间为t时,AP=t,AQ=10-2t.
∵∠QAP=∠BAO,当
| PA |
| OA |
| QA |
| BA |
△APQ∽△AOB,
| t |
| 6 |
| 10-2t |
| 10 |
∴t=
| 30 |
| 11 |
∵∠QAP=∠BAO,
∴当
| PA |
| AB |
| AQ |
| AO |
△APQ∽△AOB,
∴
| t |
| 10 |
| 10-2t |
| 6 |
∴t=
| 50 |
| 13 |
∴t=
| 30 |
| 11 |
| 50 |
| 13 |
(3)当t=
| 30 |
| 11 |
| 30 |
| 11 |
∴OP=
| 36 |
| 11 |
∴P(
| 36 |
| 11 |
∴线段PQ所在直线的函数表达式为x=
| 36 |
| 11 |
当t=
| 50 |
| 13 |
| 50 |
| 13 |
| 100 |
| 13 |
| 28 |
| 13 |
∴P(
| 28 |
| 13 |
设Q点的坐标为(x,y),则有
| X |
| OA |
| BQ |
| BA |
∴
| x |
| 6 |
| ||
| 10 |
∴x=
| 60 |
| 13 |
当x=
| 60 |
| 13 |
| 4 |
| 3 |
| 60 |
| 13 |
| 24 |
| 13 |
∴Q的坐标为(
| 60 |
| 13 |
| 24 |
| 13 |
设PQ的表达式为y=kx+b,
则
|
∴
|
∴PQ的表达式为y=
| 3 |
| 4 |
| 21 |
| 13 |
点评:此题考查的是一次函数的解析式与三角形相结合,根据三角形相似求一次函数的解析式,有一定的难度.是中学阶段的难点.

练习册系列答案
相关题目
 如图,已知直线l与坐标轴相交于点A(2,0)、B(0,-3).
如图,已知直线l与坐标轴相交于点A(2,0)、B(0,-3).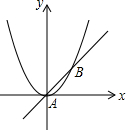 如图,已知直线y=x与抛物线y=
如图,已知直线y=x与抛物线y=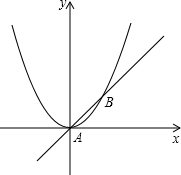 (2013•德宏州)如图,已知直线y=x与抛物线
(2013•德宏州)如图,已知直线y=x与抛物线 (2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
(2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9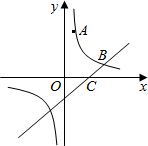 如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)
如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)