题目内容
已知质数p、q使得表达式| 2p+1 |
| q |
| 2q-3 |
| p |
分析:先设p≥q,再由
为自然数可判断出能
=1,即p=2q-3,同理由
是自然数可求出q=5,p=7;再设p<q,可求出
的取值范围,再分
=1和
=2两种情况进行讨论,找出符合条件的未知数的值代入代数式计算即可.
| 2q-3 |
| p |
| 2q-3 |
| p |
| 2p+1 |
| q |
| 2p+1 |
| q |
| 2p+1 |
| q |
| 2p+1 |
| q |
解答:解:先设p≥q,则有1≤
=2×
-
<2,于是只能
=1,即p=2q-3,
而这时
=
=4-
,要使
为自然数,只能q=5,从而p=7,
再设p<q,这时1≤
=2×
+
<3,于是有下面两种情况:
①
=1,q=2p+1,此时
=
,
解得p=1,不合题意;
②
=2,2p+1=2q,左边为奇数,右边为偶数,矛盾.
故p2q=72×5=245.
故答案为:245.
| 2q-3 |
| p |
| q |
| p |
| 3 |
| p |
| 2q-3 |
| p |
而这时
| 2p+1 |
| q |
| 4q-5 |
| q |
| 5 |
| q |
| 2p+1 |
| q |
再设p<q,这时1≤
| 2p+1 |
| q |
| p |
| q |
| 1 |
| q |
①
| 2p+1 |
| q |
| 2q-3 |
| p |
| 4p-1 |
| p |
解得p=1,不合题意;
②
| 2p+1 |
| q |
故p2q=72×5=245.
故答案为:245.
点评:本题考查的是数的整除性问题、自然数、奇数与偶数、质数的定义,涉及面较广,难度较大.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
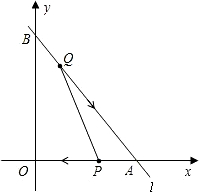 线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒