题目内容
19.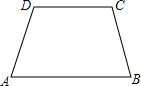 如图,梯形ABCD中,AB∥CD,AD=BC,AB=16cm,CD=10cm,高为9cm.
如图,梯形ABCD中,AB∥CD,AD=BC,AB=16cm,CD=10cm,高为9cm.(1)若A、B、C、D四点在同一圆上吗?为什么?
(2)若在同一圆上,求此圆的半径.
分析 (1)由等腰梯形的性质得出∠A+∠C=180°,即可得出A、B、C、D四点在同一圆上;
(2)作CD的垂直平分线EF,垂足为M,连接OC、OB,则EF一定经过圆心O,EF⊥AB,MN=9cm,由垂径定理得出CM、BM的长,设OM=xcm,则ON=(9-x)cm,根据勾股定理得出方程,解方程求出x,再根据勾股定理求出OC即可.
解答 解:(1)A、B、C、D四点在同一圆上;理由如下:
∵梯形ABCD中,AB∥CD,AD=BC,
∴∠A=∠B,∠C=∠D,
∵∠A+∠B+∠C+∠D=360°,
∴∠A+∠C=180°,
∴A、B、C、D四点在同一圆上;
(2)如图所示: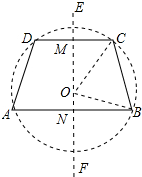 作CD的垂直平分线EF,垂足为M,连接OC、OB,
作CD的垂直平分线EF,垂足为M,连接OC、OB,
则EF一定经过圆心O,EF⊥AB,MN=9cm,
∴CM=$\frac{1}{2}$CD=5cm,BN=AN=$\frac{1}{2}$AB=8cm,
设OM=xcm,则ON=(9-x)cm,
根据勾股定理得:OC2=OM2+CM2,OB2=ON2+BM2,OC=OB,
∴x2+52=(9-x)2-82,
解得:x=$\frac{20}{3}$,
∴OC=$\sqrt{(\frac{20}{3})^{2}+{5}^{2}}$=$\frac{25}{3}$(cm),
即此圆的半径为$\frac{25}{3}$cm.
点评 本题考查了等腰梯形的性质、四点共圆、垂径定理、勾股定理等知识;本题有一定难度,特别是(2)中,需要通过作辅助线,运用勾股定理得出方程才能求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
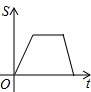
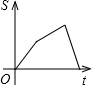
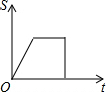
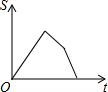
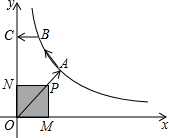 如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )