题目内容
 如图,A、B两点坐标分别为A(a,4),B(b,0),且a,b满足(a-2b+8)2+
如图,A、B两点坐标分别为A(a,4),B(b,0),且a,b满足(a-2b+8)2+| 2a+b-9 |
(1)求A、B两点坐标;
(2)若C为y轴上一点且S△AOC=
| 1 |
| 5 |
(3)过B作BD∥y轴,∠DBF=
| 1 |
| 3 |
| 1 |
| 3 |
考点:坐标与图形性质,非负数的性质:偶次方,非负数的性质:算术平方根,解二元一次方程组,平行线的性质,三角形的面积
专题:
分析:(1)直接利用偶次方以及算术平方根的定义得出二元一次方程组求出即可;
(2)利用已知点的坐标得出S△AOB=
×5×4=10,进而得出C点坐标;
(3)利用平行线的性质得出∠A=∠EOA+∠DBA,进而得出∠OFM+∠BFM=
∠DBA+
∠EOA,即可得出答案.
(2)利用已知点的坐标得出S△AOB=
| 1 |
| 2 |
(3)利用平行线的性质得出∠A=∠EOA+∠DBA,进而得出∠OFM+∠BFM=
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)∵(a-2b+8)2+
=0,
∴
,
解得:
,
∴A(2,4),B(5,0);
(2)∵A(2,4),B(5,0),
∴BO=5,
S△AOB=
×5×4=10,
∵C为y轴上一点且S△AOC=
S△AOB=2,
∴CO=2,
∴C点的坐标为:(0,2)或(0,-2);
(3)过点F作y轴的平行线
∵BD∥y轴,
∴∠EOB+∠DBO=180°,即∠EOA+∠AOB+∠ABO+∠ABD=180°,
∵∠A+∠AOB+∠ABO=180°,
∴∠A=∠EOA+∠DBA,
∵FM∥BD∥y轴,
∴∠EOF=∠OFM,∠DBF=∠BFM,
∵∠DBF=
∠DBA,∠EOF=
∠EOA,
∴∠OFM+∠BFM=
∠DBA+
∠EOA,
∴∠OFB=
∠A.
| 2a+b-9 |
∴
|
解得:
|
∴A(2,4),B(5,0);
(2)∵A(2,4),B(5,0),
∴BO=5,
S△AOB=
| 1 |
| 2 |
∵C为y轴上一点且S△AOC=
| 1 |
| 5 |
∴CO=2,
∴C点的坐标为:(0,2)或(0,-2);
(3)过点F作y轴的平行线

∵BD∥y轴,
∴∠EOB+∠DBO=180°,即∠EOA+∠AOB+∠ABO+∠ABD=180°,
∵∠A+∠AOB+∠ABO=180°,
∴∠A=∠EOA+∠DBA,
∵FM∥BD∥y轴,
∴∠EOF=∠OFM,∠DBF=∠BFM,
∵∠DBF=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠OFM+∠BFM=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠OFB=
| 1 |
| 3 |
点评:此题主要考查了坐标与图形的性质以及三角形内角和定理以及平行线的性质等知识,利用已知点的坐标得出线段长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)
小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)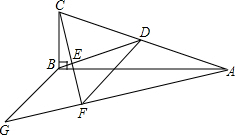 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.请解答以下两个问题.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.请解答以下两个问题.