题目内容
18．
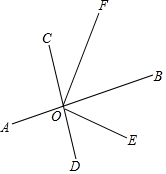如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠BOC，求∠EOF的度数．
分析 根据角平分线定义得出∠BOF=$\frac{1}{2}$∠BOC，∠BOE=$\frac{1}{2}∠BOD$，根据∠BOD+∠BOC=180°求出即可．
解答 解：∵OE平分∠BOD，OF平分∠BOC，
∴∠BOF=$\frac{1}{2}$∠BOC，∠BOE=$\frac{1}{2}∠BOD$，
∵∠BOD+∠BOC=180°，
∴$∠BOF+∠BOE=\frac{1}{2}$（∠BOC+∠BOD）=90°，
∴∠EOF=90°．
点评 本题考查了角平分线定义和邻补角等知识点能根据角平分线定义得出∠BOF=$\frac{1}{2}$∠BOC和∠BOE=$\frac{1}{2}∠BOD$是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
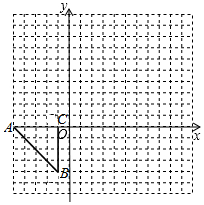如图，直角坐标系中的△ABC的三个顶点分别为A（-5，0），B（-1，-4），C（-1，0）．
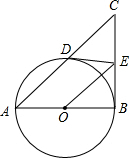如图，AB为⊙O的直径，E是⊙O外一点，过点E作⊙O的两条切线ED、EB，切点分别为点D，B，连接AD并延长交BE延长线于点C，连接OE．
6．
如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（ ）
如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（ ）| A． | 30° | B． | 32° | C． | 42° | D． | 58° |
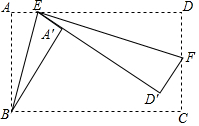如图，矩形ABCD中，AB=8，BC=15，点E是AD边上一点，连接BE，把△ABE沿BE折叠，使点A落在点A′处，点F是CD边上一点，连接EF，把△DEF沿EF折叠，使点D落在直线EA′上的点D′处，当点D′落在BC边上时，AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$．
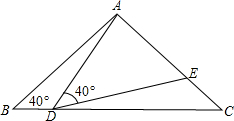如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪．如图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°