题目内容
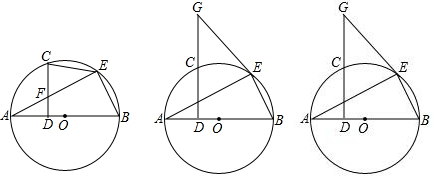
9.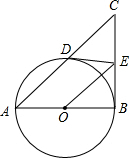 如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.
如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.(1)试判断OE与AC的关系,并说明理由;
(2)填空:
①当∠BAC=45°时,四边形ODEB是正方形.
②当∠BAC=30°时,$\frac{AD}{DE}$的值为4.
分析 (1)连接OD,根据切线的性质,由DE是⊙O的切线得到∠ODE=90°,再利用“HL”证明Rt△ODE≌Rt△OBE,得到ED=EB,∠1=∠2,由三角形外角性质得∠BOD=∠A+∠3,加上∠A=∠3,则∠2=∠4,于是可判断OE∥AC;
(2)①根据全等三角形的性质得到ED=EB,根据圆周角定理得到∠DOB=90°,于是得到结论;
②过O作OH⊥AD于H,根据等腰三角形的性质得到∠3=∠A=30°,得到OD=$\frac{\sqrt{3}}{4}$AD,得到OD=$\sqrt{3}$DE,列方程即可得到结论.
解答 解(1)OE∥AC,OE=$\frac{1}{2}$AC,
理由:连接OD,
∵DE,BE是圆O的切线,
∴OD⊥DE,AB⊥BC,
∴∠ODE=∠ABC=90°,
∵OD=OB,OE=OE,
∴Rt△ODE≌Rt△OBE(HL)
∴∠1=∠2,
∵∠BOD=∠A+∠3,OA=OD,
∴∠A=∠3,
∴∠2=∠A,
∴OE∥AC,∵OA=OB,∴EC=EB,
∴OE是△ABC的中位线,
∴OE=$\frac{1}{2}$AC,
(2)①∵Rt△ODE≌Rt△OBE,
∴ED=EB,
∵∠A=45°,
∴∠DOB=90°,
∴∠DOB=∠ODE=∠B=90°,
∴四边形ODEB是正方形;
②过O作OH⊥AD于H,
∵∠A=30°,OA=OD,
∴∠3=∠A=30°,
∴OD=$\frac{\sqrt{3}}{4}$AD,
∵∠ODE=90°,∠1=∠3=30°,
∴OD=$\sqrt{3}$DE,
∴$\frac{\sqrt{3}}{4}$AD=$\sqrt{3}$DE,
∵AD=nDE,
∴n=4.
故答案为:45°,4.
点评 本题考查了切线的性质,全等三角形的判定和性质,正方形的判定,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案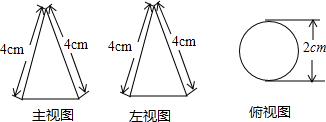
| A. | 4π | B. | 2π | C. | 4 | D. | π |
 移到了点
移到了点 .
.


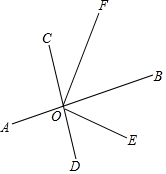 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,求∠EOF的度数. 公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在
公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在