题目内容
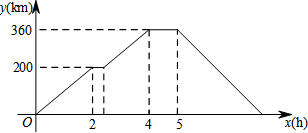
11.对于某些三角形或是四边形,我们可以直接用面积公式或是用割补法等来求它们的面积,下面我们研究一种求面积的新方法:如图1、2所示,分别过三角形或是四边形的顶点A、C作水平线的铅垂线l1、l2,l1、l2之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交AC于点D,称线段BD的长叫做这个三角形的铅垂高;如图2所示,分别过四边形的顶点B、D作水平线l3、l4,l3、l4之间的距离h叫做四边形的铅垂高.
【结论提炼】:容易证明:“三角形的面积等于水平宽与铅垂高乘积的一半”,即“S=$\frac{1}{2}$dh”.
【尝试应用】:
已知:如图3,点A(-5,2)、B(5,0)、C(0,5),则△ABC的水平宽为10,铅垂高为5,所以△ABC的面积为25.
【再探新知】:
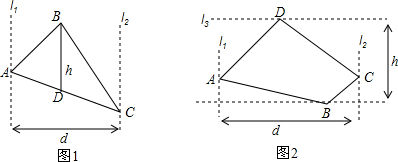
三角形的面积可以用“水平宽与铅垂高乘积的一半”来求,那四边形的面积是不是也可以这样求呢?带着这个问题,小明进行了如下探索尝试:
(1)他首先在图4所示的平面直角坐标系中,取了A(-4,2)、B(1,5)、C(4,1)、D(-1,-4)四个点,得到了四边形ABCD.
小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36;他又用其它的方法进行了计算,结果是37,由此他发现:用“S=$\frac{1}{2}$dh”这一方法对图4中的四边形求面积不适合(填“适合”或“不适合”).
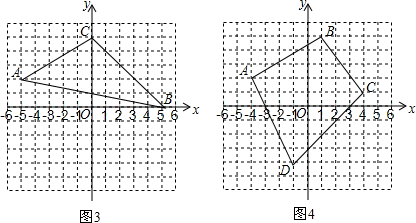
(2)小明并没有放弃尝试,他又在图5所示的平面直角坐标系中,取了A(-5,2)、B(1,5)、C(4,2)、D(-1,-3)四个点,得到了四边形ABCD.小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36,由此他发现:用“S=$\frac{1}{2}$dh”这一方法对图5中的四边形求面积适合(填“适合”或“不适合”).
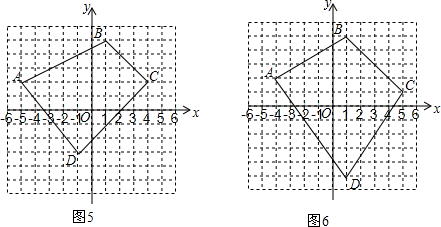
(3)小明很奇怪,就继续进行了进一步尝试,他在图6所示的平面直角坐标系中,取了A(-4,2)、B(1,5)、C(5,1)、D(1,-5)四个点,得到了四边形ABCD.通过计算他发现:用“S=$\frac{1}{2}$dh”这一方法对图6中的四边形求面积适合(填“适合”或“不适合”).
通过以上尝试,小明恍然大悟得出结论:当四边形满足一条对角线等于水平宽或铅垂高条件时,四边形可以用“S=$\frac{1}{2}$dh”来求面积.
【学以致用】:
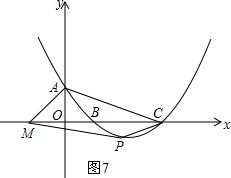
如图7,在平面直角坐标系中,点M坐标为(-2,0),抛物线的解析式为:y=$\frac{1}{4}$x2-2x+3,抛物线图象与y轴交于点A,与x轴交于B、C两点,点P为抛物线上一点,且位于B、C之间,请直接运用以上结论,写出当点P坐标为多少时,四边形AMPC面积最大.(直接写出P点坐标即可)
分析 (1)先根据面积公式或是用割补法分别求它们的面积,比较后确定面积公式“S=$\frac{1}{2}$dh”是否适合;
(2)分别用两种方法求四边形面积,比较后确定面积公式“S=$\frac{1}{2}$dh”是否适合;
(3)分别计算四边形面积,然后总结四边形的面积公式成立的条件,然后分别求出点A、M、C的坐标,根据点P为顶点时,四边形AMPC面积最大,求出顶点坐标,代入求出水平宽和铅垂高,得到四边形AMPC面积的最大值.
解答 解:(1)小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36;他又用其它的方法进行了计算,结果是37,由此他发现:用“S=$\frac{1}{2}$dh”这一方法对图4中的四边形求面积不适合;
(2)小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36,由此他发现:用“S=$\frac{1}{2}$dh”这一方法对图5中的四边形求面积适合;
(3)通过计算他发现:用“S=$\frac{1}{2}$dh”这一方法对图6中的四边形求面积适合;
结论:当四边形满足一条对角线等于水平宽或铅垂高时,四边形可以用“S=$\frac{1}{2}$dh”来求面积.
y=$\frac{1}{4}$x2-2x+3的图象与y轴交于点A(0,3),
$\frac{1}{4}$x2-2x+3=0,解得,x1=,x2=6
与x轴交点B(2,0)、C(6,0),
当P点为抛物线的顶点时,四边形AMPC面积最大,
y=$\frac{1}{4}$x2-2x+3=$\frac{1}{4}$(x-4)2-1,∴顶点的坐标为(4,-1),
四边形AMPC的水平宽为8,铅垂高为4,
∴四边形AMPC面积为:$\frac{1}{2}$×8×4=16.
点评 本题考查的是二次函数的综合运用,正确推导出四边形的面积公式和确定四边形AMPC面积最大时,点P的位置是解题的关键,本题体现了数形结合思想的运用.

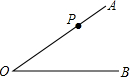 如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )
如图,P为∠AOB边OA上一点,∠AOB=30°,OP=10cm,以P为圆心,5cm为半径的圆与直线OB的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 无法确定 |
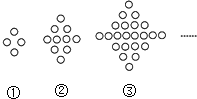 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )| A. | 46 | B. | 70 | C. | 94 | D. | 190 |
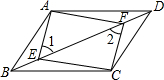 如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.
如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.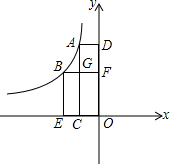 如图,点A,B是双曲线y=$\frac{k}{x}$上的点,分别经过A,B两点向x轴,y轴作垂线,垂足分别为点C,D,E,F,AC与BF交于点G,若S四边形OCGF=2,S四边形AGFD+S四边形BECG=6,则k=-5.
如图,点A,B是双曲线y=$\frac{k}{x}$上的点,分别经过A,B两点向x轴,y轴作垂线,垂足分别为点C,D,E,F,AC与BF交于点G,若S四边形OCGF=2,S四边形AGFD+S四边形BECG=6,则k=-5.
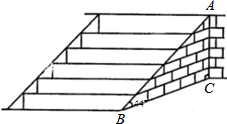 武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).
武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为5米(BC所在地面为水平面).