题目内容
 在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)
在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)考点:解直角三角形的应用
专题:
分析:如图,过点C作CE⊥AB于点E.通过解Rt△EAC和Rt△EBC分别求得AE、BE的长度,然后根据图示知:AB=BE-AE=100,把相关线段的长度代入列出关于EC的方程
-
=100,通过解该方程求得EC的长度.
| EC |
| tan60° |
| EC |
| tan75° |
解答: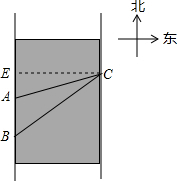 解:如图,过点C作CE⊥AB于点E.
解:如图,过点C作CE⊥AB于点E.
∵在Rt△EAB中,∠CBE=60°,
∴tan60°=
,
∴BE=
,
同理,在Rt△EAC中,
得到EA=
.
又∵AB=100米,
∴BE-EA=100米,
即
-
=100.
则ED=
≈
≈323(米).
答:点C到河西岸的距离.
 解:如图,过点C作CE⊥AB于点E.
解:如图,过点C作CE⊥AB于点E.∵在Rt△EAB中,∠CBE=60°,
∴tan60°=
| CE |
| BE |
∴BE=
| CE |
| tan60° |
同理,在Rt△EAC中,
得到EA=
| EC |
| tan75° |
又∵AB=100米,
∴BE-EA=100米,
即
| CE |
| tan60° |
| EC |
| tan75° |
则ED=
| 100×tan60°×tan75° |
| tan75°-tan60° |
| 100×1.73×1.73 |
| 3.73-1.73 |
答:点C到河西岸的距离.
点评:本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
 如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )
如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )| A、2 | B、4 | C、8 | D、1 |
下列成语所描述的事件中是随机事件的是( )
| A、水中捞月 | B、拔苗助长 |
| C、守株待兔 | D、瓮中捉鳖 |
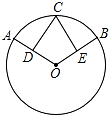 如图,D、E分别是半径OA和OB的中点,
如图,D、E分别是半径OA和OB的中点,
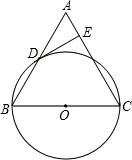 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E. 已知平行四边形ABCD的面积是36平方厘米,DE⊥AB,AB=9cm,BE=3cm,求△AED的面积.
已知平行四边形ABCD的面积是36平方厘米,DE⊥AB,AB=9cm,BE=3cm,求△AED的面积.