题目内容
已知a1=x,an+1=1-
(n为正整数),则a2013= .
| 1 |
| an |
考点:规律型:数字的变化类
专题:
分析:利用数列递推式,确定数列an,进一步找出规律,利用规律,即可求出a2013的值.
解答:解:∵a1=x,
a2=1-
=
,
a3=1-
=-
,
a4=1-(-x+1)=x,
…
∴数列{an}是周期为3的数列,
∵2013÷3=671
∴a2013=a3=-
.
故答案为:-
.
a2=1-
| 1 |
| x |
| x-1 |
| x |
a3=1-
| x |
| x-1 |
| 1 |
| x-1 |
a4=1-(-x+1)=x,
…
∴数列{an}是周期为3的数列,
∵2013÷3=671
∴a2013=a3=-
| 1 |
| x-1 |
故答案为:-
| 1 |
| x-1 |
点评:此题考查数字的排列规律,找出数字之间的联系,发现规律,解决问题.

练习册系列答案
相关题目
 如图,直线y=x+1与y轴相交于点A,四边形OABC和四边形CDEF都是正方形,则点E的坐标为( )
如图,直线y=x+1与y轴相交于点A,四边形OABC和四边形CDEF都是正方形,则点E的坐标为( )| A、(3,2) | ||
| B、(2,3) | ||
C、(2
| ||
| D、(5,4) |
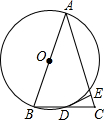 如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E. 如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,则四边形ADEF的周长为
如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,则四边形ADEF的周长为