题目内容
11.阅读材料:已知分式$\frac{3n+8}{n+1}$,化简后结果是整数,符合一切整数的n有哪些?解:∵$\frac{3n+8}{n+1}$=$\frac{3n+3+5}{n+1}$=3+$\frac{5}{n+1}$.
∴只要求出$\frac{5}{n+1}$是整数,则n+1是5的约数,即n+1=5,n+1=1,n+1=-5,n+1=1.
∴n1=4,n2=0,n3=-6,n4=2.
(1)已知分式$\frac{2n+9}{n+1}$,化简后结果是整数,符合要求的整数n有哪些?
(2)已知分式$\frac{3{n}^{2}+7n+7}{n+2}$,化简后结果是整数,符合要求的整数n有哪些?
分析 (1)将2n+9写成2n+2+7即2(n+1)+7,类比题意可得整数n的值;
(2)将分子分解因式3n2+7n+7=3n2+7n+2+5=(3n+1)(n+2)+5,类比题意可得整数n的值.
解答 解:(1)∵$\frac{2n+9}{n+1}=\frac{2n+2+7}{n+1}=2+\frac{7}{n+1}$,
∴只要求出$\frac{7}{n+1}$是整数,则n+1是7的约数,即n+1=7,n+1=1,n+1=-7,n+1=-1.
∴n1=6,n2=0,n3=-8,n4=-2.
(2)∵$\frac{3{n}^{2}+7n+7}{n+2}$=$\frac{3{n}^{2}+7n+2+5}{n+2}=\frac{(3n+1)(n+2)+5}{n+2}$=$3n+1+\frac{5}{n+2}$,
∴只要求出$\frac{5}{n+2}$是整数,则n+2=5,n+2=1,n+2=-5,n+2=-1.
∴n1=3,n2=-1,n3=-7,n4=-3.
点评 本题主要考查分式的变形规律和分式性质的应用能力,将分子变形是解题关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
(1)观察条形统计图,可以发现:八年级成绩的标准差<,七年级成绩的标准差(填“>”、“<”或“=”),表格中m=6,n=7.5;
(2)计算七年级的平均分;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | m | 3.41 | 90% | 20% | |
| 八年级 | 7.1 | n | 80% | 10% |
(2)计算七年级的平均分;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
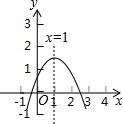 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论: 如图,在△ABC中,AD是BC边上的中线,点F在AC上,AF=$\frac{1}{2}$FC,AD与BF交于点E.求证:点E是AD的中点.
如图,在△ABC中,AD是BC边上的中线,点F在AC上,AF=$\frac{1}{2}$FC,AD与BF交于点E.求证:点E是AD的中点. 如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号)
如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号)