题目内容
2．先化简，再求值：$\frac{{x}^{2}-2x+1}{{x}^{2}-x}$-$\frac{{x}^{2}-4}{{x}^{2}+2x}$+$\frac{1}{x}$，其中x=$\sqrt{3}$-1．分析 原式前两项约分后，利用同分母分式的加减法则计算得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{（x-1）^{2}}{x（x-1）}$-$\frac{（x+2）（x-2）}{x（x+2）}$+$\frac{1}{x}$
=$\frac{x-1}{x}$-$\frac{x-2}{x}$+$\frac{1}{x}$
=$\frac{x-1-x+2+1}{x}$
=$\frac{2}{x}$，
当x=$\sqrt{3}$-1时，原式=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
12．
如图是某几何体的三视图，则该几何体是（ ）
如图是某几何体的三视图，则该几何体是（ ）| A． | 正方体 | B． | 圆锥体 | C． | 圆柱体 | D． | 球体 |
13．对于解不等式$-\frac{2x}{3}＞\frac{3}{2}$，正确的结果是（ ）
| A． | $x＜-\frac{9}{4}$ | B． | $x＞-\frac{9}{4}$ | C． | x＞-1 | D． | x＜-1 |
10．如果a＞b，那么下列不等式一定成立的是（ ）
| A． | a-b＜0 | B． | -a＞-b | C． | $\frac{1}{2}$a＜$\frac{1}{2}$b | D． | 2a＞2b |
7．某公司三月份的产值为a万元，比二月份增长了m%，那么二月份的产值（单位：万元）为（ ）
| A． | a（1+m%） | B． | a（1-m%） | C． | $\frac{a}{1+m%}$ | D． | $\frac{a}{1-m%}$ |
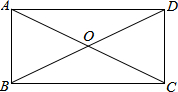如图，在四边形ABCD中，AC、BD交于点O，AO=CO，BO=DO，∠ABC=∠DCB．