题目内容
（2013•潮南区模拟）已知扇形的圆心角为120°，面积为300πcm2，若用该扇形围成一个圆锥，则该圆锥底面圆的半径为
10
10
cm．分析：利用扇形的面积公式即可求得扇形的半径，然后利用弧长公式即可求得扇形的弧长，最后根据圆的周长公式即可求解．
解答：解：设扇形的半径是R，则
=300π，解得：R=30，
则扇形的弧长是：
=20π，
设圆锥底面圆的半径为r，则2πr=20π，解得r=10．
故答案是：10．
| 120πR2 |
| 360 |
则扇形的弧长是：
| 120π×30 |
| 180 |
设圆锥底面圆的半径为r，则2πr=20π，解得r=10．
故答案是：10．
点评：本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
练习册系列答案
相关题目
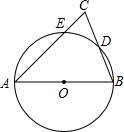（2013•潮南区模拟）如图，AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD，∠C=70°，现给出以下四个结论：