题目内容
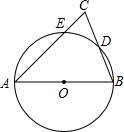（2013•潮南区模拟）如图，AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD，∠C=70°，现给出以下四个结论：①∠A=45°；②AC=AB；③
 |
| AE |
|
| BE |
其中正确结论的个数为（ ）
分析：连接AD，由AB为圆O的直径，利用直径所对的圆周角为直角得到AD垂直于BC，再由D为BC的中点，利用线段垂直平分线定理得到AC=BC，故②正确，再利用等边对等角得到∠B=∠C，利用三角形内角和定理求出∠A的度数，即可对于①作出判断；连接ED，利用圆内接四边形的外角等于它的内对角，得到两对角线段，利用两对对应角相等的两三角形相似，得到三角形CDE与三角形ABC相似，由相似得比例，即可对于④中的式子作出判断；连接OE，OE不一定与AB垂直，故弧AE不一定等于弧BE，即可得到正确的选项．
解答：
解：连AD，ED，OE，
∵AB为圆O的直径，
∴∠ADB=90°，
∴AD⊥BC，
∵CD=BD，
∴AD垂直平分BC，
∴AC=AB，故选项②正确；
∴∠B=∠C=70°，
∴∠BAC=180°-70°-70°=40°，故选项①错误；
∵四边形AEDB为圆O的内接四边形，
∴∠CED=∠B，∠CDE=∠BAC，
∴△CDE∽△CAB，
∴
=
，即CA•CE=CD•CB，
又CA=AB，CD=BD=
BC，
则CE•AB=2BD2，故选项④正确；
而EO不一定垂直于AB，故选项③错误，
则其中正确的有2个．
故选B
解：连AD，ED，OE，∵AB为圆O的直径，
∴∠ADB=90°，
∴AD⊥BC，
∵CD=BD，
∴AD垂直平分BC，
∴AC=AB，故选项②正确；
∴∠B=∠C=70°，
∴∠BAC=180°-70°-70°=40°，故选项①错误；
∵四边形AEDB为圆O的内接四边形，
∴∠CED=∠B，∠CDE=∠BAC，
∴△CDE∽△CAB，
∴
| CD |
| CA |
| CE |
| CB |
又CA=AB，CD=BD=
| 1 |
| 2 |
则CE•AB=2BD2，故选项④正确；
而EO不一定垂直于AB，故选项③错误，
则其中正确的有2个．
故选B
点评：此题考查了圆周角定理，垂径定理，相似三角形的判定与性质，以及圆内接四边形的性质，熟练掌握定理是解本题的关键．
练习册系列答案
53随堂测系列答案
相关题目