题目内容
16.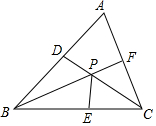 如图,在△ABC中,D,E,F分别在边AB,BC,AC上,BD=BE,CE=CF,连接BF,CD相交于点P,BF,CD恰好是△ABC的角平分线.
如图,在△ABC中,D,E,F分别在边AB,BC,AC上,BD=BE,CE=CF,连接BF,CD相交于点P,BF,CD恰好是△ABC的角平分线.(1)求证:PD=PF;
(2)求∠A的度数.
分析 (1)根据角平分线的定义可得∠ABP=∠CBP,再利用“边角边”证明△BDP和△BEP全等,根据全等三角形对应边相等可得PD=PE,同理可得PE=PF,然后等量代换即可得证;
(2)根据全等三角形对应角相等可得∠BPD=∠BPE,同理可得∠CPE=∠CPF,从而得到∠BPC=2∠BPD,再根据平角等于180°列方程求出∠BPD=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PBC+∠PCB,再根据角平分线的定义求出∠ABC+∠ACB,然后利用三角形的内角和等于180°列式求解即可.
解答 (1)证明:∵BF是△ABC的平分线,
∴∠ABP=∠CBP,
在△BDP和△BEP中,$\left\{\begin{array}{l}{BD=BE}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$,
∴△BDP≌△BEP(SAS),
∴PD=PE,
同理可得PE=PF,
∴PD=PF;
(2)∵△BDP≌△BEP,
∴∠BPD=∠BPE,
同理可得∠CPE=∠CPF,
∵∠BPD=∠CPF(对顶角相等),
∴∠BPD=∠BPE=∠CPE=∠CPF,
∴∠BPC=2∠BPD,
∵∠BPC+∠BPD-180°,
∴∠BPD=60°,
由三角形的外角性质得,∠BPD=∠PBC+∠PCB=60°,
∵BF,CD恰好是△ABC的角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∴∠ABC+∠ACB=2(∠PBC+∠PCB)=2×60°=120°,
在△ABC中,∠A=180°-(∠ABC+∠ACB)=180°-120°=60°.
点评 本题考查了全等三角形的判定与性质,角平分线的定义,三角形的内角和定理,熟练掌握三角形全等的判定方法是解题的关键,(2)要注意整体思想的利用.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案

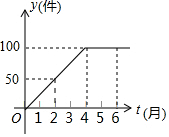 如图是某工厂在2014年前6个月生产某产品的总产量y(件)和时间t(月)的关系的图象,根据图象回答下列问题:
如图是某工厂在2014年前6个月生产某产品的总产量y(件)和时间t(月)的关系的图象,根据图象回答下列问题: 如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长.
如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长. 如图,已知平行四边形ABCD及对角线BD,求作△BCD关于直线BD的对称图形(不要求写作法).
如图,已知平行四边形ABCD及对角线BD,求作△BCD关于直线BD的对称图形(不要求写作法).