题目内容
如图①,在平面直角坐标系中,直线y=-
x+
与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
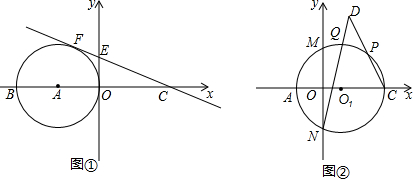
(1)求⊙A的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
| ||
| 4 |
| ||
| 2 |
(1)求⊙A的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
考点:圆的综合题,平行线的判定,全等三角形的判定与性质,勾股定理
专题:综合题
分析:(1)连接AF,如图①a,由直线EC的解析式可求出OE、OC的长,根据勾股定理可求出EC的长,然后根据切线长定理可求出EF的长,然后在Rt△AFC中运用勾股定理就可求出圆的半径.
(2)连接OF,交AE于点H,如图①b,根据切线长定理可得EF=EO,EA平分∠FEO,根据等腰三角形的性质可得∠AHO=90°,由BO是⊙A的直径可得∠BFO=90°,从而得到∠BFO=∠AHO,即可得到BF∥AE.
(3)连接QC、QM、MC、NC、MO1,如图②,易证△MCQ≌△DCQ,则有MC=DC.在Rt△MOO1中,运用勾股定理可求出MO的长,然后在Rt△MOC中,运用勾股定理就可求出MC,即可得到CD的长.
(2)连接OF,交AE于点H,如图①b,根据切线长定理可得EF=EO,EA平分∠FEO,根据等腰三角形的性质可得∠AHO=90°,由BO是⊙A的直径可得∠BFO=90°,从而得到∠BFO=∠AHO,即可得到BF∥AE.
(3)连接QC、QM、MC、NC、MO1,如图②,易证△MCQ≌△DCQ,则有MC=DC.在Rt△MOO1中,运用勾股定理可求出MO的长,然后在Rt△MOC中,运用勾股定理就可求出MC,即可得到CD的长.
解答:解:(1)连接AF,如图①a.
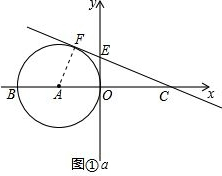
∵直线y=-
x+
与x轴交于C点,与y轴交于E点,
∴点C的坐标为(2,0),点E的坐标为(0,
),
∴OC=2,OE=
.
∵∠EOC=90°,
∴EC=
=
.
∵AO⊥OE,∴直线OE与⊙A相切于点O.
又∵直线CE与⊙A相切于点F,
∴∠AFC=90°,EF=OE=
,
∴FC=FE+EC=
+
=2
.
在Rt△AFC中,
设AF=x,则AO=x,AC=x+2.
根据勾股定理可得:x2+(2
)2=(x+2)2,
解得:x=1.
∴⊙A的半径为1.
(2)BF∥AE.
证明:连接OF,交AE于点H,如图①b.
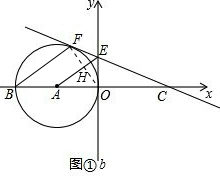
∵EF、EO分别与⊙A相切于点F、O,
∴EF=EO,EA平分∠FEO,
∴EA⊥OF,即∠AHO=90°.
∵BO是⊙A的直径,
∴∠BFO=90°,
∴∠BFO=∠AHO,
∴BF∥AE.
(3)连接QC、QM、MC、NC、MO1,如图②.
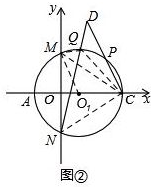
∵AC是⊙O1的直径,AC⊥MN,
∴
=
,
∴∠NQC=∠MNC.
∵∠MQC+∠MNC=180°,∠DQC+∠NQC=180°,
∴∠MQC=∠DQC.
∵点Q是
的中点,
∴∠MCQ=∠PCQ.
在△MCQ和△DCQ中,
,
∴△MCQ≌△DCQ(ASA),
∴MC=DC.
∵OA=1,OC=2,
∴AC=3,AO1=
,OO1=
,
在Rt△MOO1中,
MO1=AO1=
,OO1=
,
∴MO=
=
.
在Rt△MOC中,
MC=
=
,
∴DC=
.
∴CD的长为
.

∵直线y=-
| ||
| 4 |
| ||
| 2 |
∴点C的坐标为(2,0),点E的坐标为(0,
| ||
| 2 |
∴OC=2,OE=
| ||
| 2 |
∵∠EOC=90°,
∴EC=
| OE2+OC2 |
3
| ||
| 2 |
∵AO⊥OE,∴直线OE与⊙A相切于点O.
又∵直线CE与⊙A相切于点F,
∴∠AFC=90°,EF=OE=
| ||
| 2 |
∴FC=FE+EC=
| ||
| 2 |
3
| ||
| 2 |
| 2 |
在Rt△AFC中,
设AF=x,则AO=x,AC=x+2.
根据勾股定理可得:x2+(2
| 2 |
解得:x=1.
∴⊙A的半径为1.
(2)BF∥AE.
证明:连接OF,交AE于点H,如图①b.

∵EF、EO分别与⊙A相切于点F、O,
∴EF=EO,EA平分∠FEO,
∴EA⊥OF,即∠AHO=90°.
∵BO是⊙A的直径,
∴∠BFO=90°,
∴∠BFO=∠AHO,
∴BF∥AE.
(3)连接QC、QM、MC、NC、MO1,如图②.

∵AC是⊙O1的直径,AC⊥MN,
∴
 |
| NC |
 |
| MC |
∴∠NQC=∠MNC.
∵∠MQC+∠MNC=180°,∠DQC+∠NQC=180°,
∴∠MQC=∠DQC.
∵点Q是
 |
| MP |
∴∠MCQ=∠PCQ.
在△MCQ和△DCQ中,
|
∴△MCQ≌△DCQ(ASA),
∴MC=DC.
∵OA=1,OC=2,
∴AC=3,AO1=
| 3 |
| 2 |
| 1 |
| 2 |
在Rt△MOO1中,
MO1=AO1=
| 3 |
| 2 |
| 1 |
| 2 |
∴MO=
| MO12-OO12 |
| 2 |
在Rt△MOC中,
MC=
| MO2+OC2 |
| 6 |
∴DC=
| 6 |
∴CD的长为
| 6 |
点评:本题考查了圆周角定理、切线长定理、切线的性质、圆内接四边形的性质、全等三角形的判定与性质、平行线的判定、勾股定理等知识,而通过证明△MCQ≌△DCQ得到MC=DC是解决第(3)小题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
| A、3个 | B、2个 | C、1个 | D、0个 |
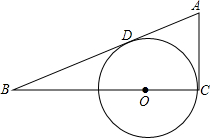 在Rt△ABC中,∠C=90°,AC=3,BC=4,O为BC上一点,以O为圆心,OC为半径作⊙O与AB相切于D,则⊙O的半径为
在Rt△ABC中,∠C=90°,AC=3,BC=4,O为BC上一点,以O为圆心,OC为半径作⊙O与AB相切于D,则⊙O的半径为