题目内容
甲同学骑车从学校到火车站,乙同学骑车从火车站回学校,甲骑车比乙每小时快2千米,两人在上午8点同时出发,到上午10点两人相距36千米,到中午1点两人又相距36千米,求学校和火车站的距离.
考点:一元一次方程的应用
专题:
分析:设乙的速度为x千米/时,则甲的速度为(x+2)千米/时,根据行程问题的数量关系甲、乙行驶的路程与甲、乙的位置关系建立方程求出其解就可以求出结论.
解答:解:设乙的速度为x千米/时,则甲的速度为(x+2)千米/时,由题意,得
(10-8)(x+x+2)+36=(13-8)(x+x+2)-36,
解得:x=11,
∴甲的速度为:11+2=13千米/时.
∴学校和火车站的距离为:2×(11+11+2)+36=84千米.
答:学校和火车站的距离为:84千米.
(10-8)(x+x+2)+36=(13-8)(x+x+2)-36,
解得:x=11,
∴甲的速度为:11+2=13千米/时.
∴学校和火车站的距离为:2×(11+11+2)+36=84千米.
答:学校和火车站的距离为:84千米.
点评:本题考查了行程问题的数量关系的运用,一元一次方程的解法的运用,解答时由路程相等建立方程是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
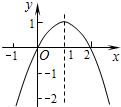 如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是
如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是