题目内容
1.在探索有关整式的乘法法则时,可以借助几何图形来解释某些法则.例如,平方差公式可以用图形①来解释.实际上还有些代数式恒等式也可以用这种形式表示,例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图②中的几何图形的面积来表示.(1)请写出图③中的几何图形所表示的代数恒等式(2a+b)(a+2b)=2a2+5ab+2b2;
(2)试画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述方法另写一个含有a,b的代数恒等式,并画出与之相对应的几何图形.

分析 (1)利用矩形的面积相等列关系式即可;
(2)画一个长为(a+3b),宽为(a+b)的矩形即可;
(3)一个含有a,b的代数恒等式可以是(a+2b)(a+b)=a2+3ab+2b2,然后画一个长为(a+2b),宽为(a+b)的矩形即可.
解答 解:(1)根据图形可得:
(2a+b)(a+2b)=2a2+5ab+2b2;
故答案为:(2a+b)(a+2b)=2a2+5ab+2b2;
(2)画图如下(答案不唯一):
(3)恒等式是(a+2b)(a+b)=a2+3ab+2b2,如图所示(答案不唯一).
点评 本题考查了完全平方公式的几何背景,多项式乘以多项式,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.

练习册系列答案
相关题目
16.下列多项式的乘法汇总,能用平方差公式计算的是( )
| A. | (3a+2b)(2a-3b) | B. | (3a-b)(-3a-b) | C. | (-a+b)(a-b) | D. | (x-2y)(-2y+x) |
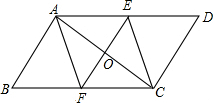 如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.
如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.