题目内容
如图，在矩形ABCD中，AB=2，AD=4，将矩形ABCD沿直线EF折叠，D到G得位置，C到H得位置，BC交EG于M点．则图中四边形ABME和四边形GHFM的周长和是（ ）A、4
| ||
B、8
| ||
| C、10 | ||
| D、12 |
考点：翻折变换（折叠问题）
专题：
分析：根据翻折前后对应边相等可得：EG=ED，GH=CD，FH=FC，从而将四边形ABME和四边形GHFM的周长转化为求矩形ABCD的周长．
解答：解：由折叠的性质可得：EM=ED，GH=FC，FH=FC，
则四边形ABME和四边形GHFM的周长和=AB+AE+BM+EM+GM+MF+FH+GH=AD+AB+BC+CD=4+2+4+2=12．
故选D．
则四边形ABME和四边形GHFM的周长和=AB+AE+BM+EM+GM+MF+FH+GH=AD+AB+BC+CD=4+2+4+2=12．
故选D．
点评：本题考查了翻折变换的性质，解答本题的关键是掌握翻折变换的性质：翻折前后对应边相等，难度一般．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
如图，在四边形ABCD中，AB=4，CD=13，DE=12，∠DAB=∠DEC=90°，∠ABE=135°，四边形ABCD的面积是（ ）| A、94 | B、90 | C、84 | D、78 |
如图，一棵树AB的顶端A的影子落在教学楼前的坪地C处，小明分别测得坪地、台阶和地面上的三段影长CE=1m，DE=2m，BD=8m，DE与地面的夹角α=30°．在同一时刻，已知一根1m长的直立竹竿在地面上的影长恰好为2m，请你帮助小明根据以上数据求出树AB的高．（结果精确到0.1m，参考数据：下列二次根式中，化简后被开方数与
的被开方数相同的是（ ）
| 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图：BC⊥AD，垂足为D．若∠A=21°，∠B=42°，求∠C和∠AEF的度数．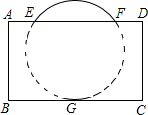
把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示．圆O与纸盒交于E、F、G三点，已知EF=CD=16cm．