题目内容
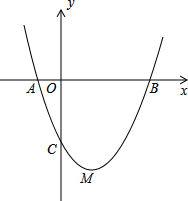 如图,在直角坐标系xOy中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴交于点C,顶点为M,已知A(-1,0).
如图,在直角坐标系xOy中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴交于点C,顶点为M,已知A(-1,0).(1)则顶点M的坐标为
(2)当y>0时,试写出x的范围,并求A、B两点间的距离;
(3)在抛物线曲线段BMC上有一动点D,求四边形OBDC面积的最大值.
考点:抛物线与x轴的交点,二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)把A点坐标代入可求得二次函数的解析式,可求得顶点坐标;
(2)可先求得A、B两点的坐标,根据图象可写出满足条件的x的取值范围,可求得AB的距离;
(3)根据题意可知△BOC面积不变,所以当D点离BC越远则△BCD的面积越大,可平移直线BC,当直线与抛物线只有一个交点时,交点即为D,再求其面积即可.
(2)可先求得A、B两点的坐标,根据图象可写出满足条件的x的取值范围,可求得AB的距离;
(3)根据题意可知△BOC面积不变,所以当D点离BC越远则△BCD的面积越大,可平移直线BC,当直线与抛物线只有一个交点时,交点即为D,再求其面积即可.
解答:解:
(1)∵抛物线过A点,
∴1-b-3=0,解得b=-2,
∴抛物线为y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4),
故答案为:(1,-4);
(2)由(1)可知抛物线解析式为y=x2-2x-3,
令y=0可得x2-2x-3=0,解得x=3或x=-1,
∴当y>0时,x<-1或x>3,
且A(-1,0),B(3,0),
∴AB=3-(-1)=4;
(3)由题意可知C(0,-3),B(3,0),
可设直线BC解析式为y=kx-3,把B点坐标代入可求得k=1,
∴直线BC解析式为y=x-3,
把直线BC向下平移,得到直线B′C′,可设直线B′C′的解析式为y=x+m,
∵△BOC面积不变,
∴当D点离直线BC越远,四边形OBDC的面积越大,
∴当直线B′C′与抛物线只有一个交点时,交点即为D点,
联立直线B′C′和抛物线的解析式,消去y可得x2-3x-3-m=0,
根据题意可知△=0,即9+4(3+m)=0,解得m=-
,
代入可求得x=
,∴D为(
,-
),
如图,过D作DE⊥y轴于点E,则OE=
,DE=
,CE=
,
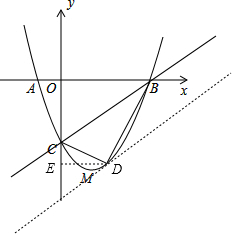
∴S四边形OBDC=S梯形OBDE-S△CDE=
(OB+DE)OE-
DE•CE=
×(3+
)×
-
×
×
=
,
综上可知四边形OBDC的最大值为
.
(1)∵抛物线过A点,
∴1-b-3=0,解得b=-2,
∴抛物线为y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4),
故答案为:(1,-4);
(2)由(1)可知抛物线解析式为y=x2-2x-3,
令y=0可得x2-2x-3=0,解得x=3或x=-1,
∴当y>0时,x<-1或x>3,
且A(-1,0),B(3,0),
∴AB=3-(-1)=4;
(3)由题意可知C(0,-3),B(3,0),
可设直线BC解析式为y=kx-3,把B点坐标代入可求得k=1,
∴直线BC解析式为y=x-3,
把直线BC向下平移,得到直线B′C′,可设直线B′C′的解析式为y=x+m,
∵△BOC面积不变,
∴当D点离直线BC越远,四边形OBDC的面积越大,
∴当直线B′C′与抛物线只有一个交点时,交点即为D点,
联立直线B′C′和抛物线的解析式,消去y可得x2-3x-3-m=0,
根据题意可知△=0,即9+4(3+m)=0,解得m=-
| 21 |
| 4 |
代入可求得x=
| 3 |
| 2 |
| 3 |
| 2 |
| 19 |
| 4 |
如图,过D作DE⊥y轴于点E,则OE=
| 19 |
| 4 |
| 3 |
| 2 |
| 7 |
| 4 |

∴S四边形OBDC=S梯形OBDE-S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 19 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 4 |
| 75 |
| 8 |
综上可知四边形OBDC的最大值为
| 75 |
| 8 |
点评:本题主要考查待定系数法求函数解析式及二次函数与一元二次方程的关系数、函数的交点等问题,掌握待定系数法求函数解析式的关键是求得点的坐标,在(3)中确定出四边形OBDC面积最大时的点D的位置是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知点A的坐标为(1,2),点B的坐标为(2,2),反比列函数y=
的图象与线段AB相交.则k的取值范围为( )
| k |
| x |
| A、k<2 | B、k≤4 |
| C、k<2或k>4 | D、2≤k≤4 |
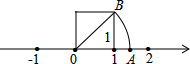 如图,OB是以数轴的单位长度为边的正方形的对角线,以数轴的原点为圆心、OB长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
如图,OB是以数轴的单位长度为边的正方形的对角线,以数轴的原点为圆心、OB长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )A、1
| ||
B、
| ||
C、
| ||
| D、1.4 |
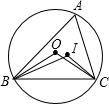 如图,△ABC中,O为△ABC的外心,I为△ABC的内心,设∠BOC=y1°,∠BIC=y2°,∠A=x°(∠BOC≤180°).
如图,△ABC中,O为△ABC的外心,I为△ABC的内心,设∠BOC=y1°,∠BIC=y2°,∠A=x°(∠BOC≤180°).