题目内容
10.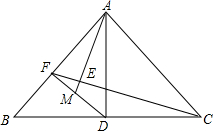 在△ABC中,AB=AC,AD⊥BC于D,DF⊥AB于F,AE⊥CF于E且交DF于M,求证:M为DF的中点.
在△ABC中,AB=AC,AD⊥BC于D,DF⊥AB于F,AE⊥CF于E且交DF于M,求证:M为DF的中点.
分析 根据垂直的定义得到∠AFD=∠DFB=90°,根据余角的性质得到∠ADF=∠B,推出△ADF∽△DBF,根据相似三角形的性质得到$\frac{AD}{BD}=\frac{DF}{BF}$,由于△ADM∽△CBF,由相似三角形的性质得到$\frac{AD}{CB}=\frac{DM}{BF}$,根据已知条件得到BD=1/2BC 等量代换得到$\frac{DF}{BF}=\frac{2DM}{BF}$,即可得到结论.
解答 证明:∵DF⊥AB于F,
∴∠AFD=∠DFB=90°,
∵AD⊥BC于D,
∴∠B+∠BDF=∠BDF+∠ADF=90°,
∴∠ADF=∠B,
∴△ADF∽△DBF,
∴$\frac{AD}{BD}=\frac{DF}{BF}$,
∵AE⊥CF,
∴∠DAM=∠FCB,
∵∠ADF=∠B,
∴△ADM∽△CBF,
∴$\frac{AD}{CB}=\frac{DM}{BF}$,
又∵BD=1/2BC,
∴$\frac{AD}{2BD}$=$\frac{DM}{BF}$,
∴$\frac{AD}{BD}=\frac{2DM}{BF}$,
∴$\frac{DF}{BF}=\frac{2DM}{BF}$,
∴DM=$\frac{1}{2}$DF,即M为DF中点.
点评 本题考查了相似三角形的判定和性质,垂直的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
19. 如图,在△ABC中,点D,E分别在边AB,AC上,且$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则三角形ADE周长与三角形ABC的周长比是( )
如图,在△ABC中,点D,E分别在边AB,AC上,且$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则三角形ADE周长与三角形ABC的周长比是( )
 如图,在△ABC中,点D,E分别在边AB,AC上,且$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则三角形ADE周长与三角形ABC的周长比是( )
如图,在△ABC中,点D,E分别在边AB,AC上,且$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$,则三角形ADE周长与三角形ABC的周长比是( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
 如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.
如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.