题目内容

19．如图，在△ABC中，点D，E分别在边AB，AC上，且$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$，则三角形ADE周长与三角形ABC的周长比是（　　）
A．1：$\sqrt{3}$B．1：2C．1：3D．1：4

分析 根据相似三角形的判定定理得到△ADE∽△ACB，然后根据相似三角形的性质即可得到结论．

解答 解：∵$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$，∠A=∠A，
∴△ADE∽△ACB，
∴三角形ADE周长与三角形ABC的周长比=$\frac{AD}{AC}=\frac{1}{2}$．
故选B．

点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．

练习册系列答案
相关题目
4．当m=3时，一次函数y=（m+2）x+3-m的图象经过原点．
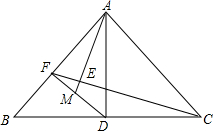10．在△ABC中，AB=AC，AD⊥BC于D，DF⊥AB于F，AE⊥CF于E且交DF于M，求证：M为DF的中点．
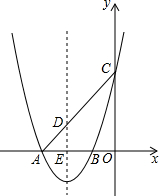7．如图，抛物线y=x2+4x+3交x轴于A，B两点（A在B左侧），交y轴于点C．已知一次函数y=kx+b的图象过点A，C．
（1）求抛物线的对称轴和一次函数的解析式；
（2）根据图象，写出满足kx+b＞x2+4x+3的x的取值范围；
（3）在平面直角坐标系xOy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由．
14．请阅读下列材料：若x1，x2是关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根，则方程的两个根x1，x2和系数a，b，c有如下关系：x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$，我们把它们称为根与系数关系定理．
如果设二次函数y=ax2+bx+c（a≠0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．利用根与系数关系定理我们又可以得到A、B两个交点间的距离为：AB=|x1-x2|=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{（-\frac{b}{a}）^{2}-\frac{4c}{a}}$=$\sqrt{\frac{{b}^{2}-4ac}{{a}^{2}}}$=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$
请你参考以上定理和结论，解答下列问题：
设二次函数y=ax2+bx+c（a＞0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．，抛物线的顶点为C，显然△ABC为等腰三角形．
（1）当△ABC为等腰直角三角形时，求b2-4ac的值；
（2）当△ABC为等边三角形时，求b2-4ac的值；
（3）设抛物线y=x2+kx+1与x轴的两个交点为A、B，顶点为C，且∠ACB=90°，试问如何平移此抛物线，才能使∠ACB=60°？
4．我们居住的地球的半径约为6400千米，这里的“6400”属于（　　）
A．记数B．测量结果C．标号D．排序
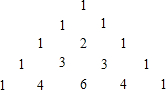11．我国宋朝数学家杨辉在他的著作《详解九章算法》中提出右下表，此表揭示了（a+b）n（n为非负整数）展开式的各项系数的规律，例如：
（a+b）0=1，它只有一项，系数为1；（a+b）1=a+b，它有两项，系数分别为1，1；（a+b）2=a2+2ab+b2，它有三项，系数分别为1，2，1；（a+b）3=a3+3a2b+3ab2+b3，它有四项，系数分别为1，3，3，1；（a+b）4=a4+4a3b+6a2b2+4ab3+b4，它有五项，系数分别为1，4，6，4，1；
根据以上规律，（a+b）5展开的结果为a5+5a4b+10a3b2+10a2b3+5ab4+b5．
8．江阴和新疆的距离约为3770000m，这个数用科学记数法可表示为3.77×107m．
9．已知等腰三角形的两边长分别为5和9，则它的周长是19或23．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网