题目内容
15. 如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.
如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.
分析 根据平行线分线段成比例得到$\frac{AD}{BD}=\frac{AE}{CE}$=$\frac{2}{1}$,于是得到$\frac{AE}{AC}$=$\frac{2}{3}$,求得S△ADE=$\frac{2}{3}$S△ADC,由于$\frac{AD}{BD}$=$\frac{2}{1}$,求得S△BDC=$\frac{1}{2}$S△ACD,即可得到结论.
解答 解:∵DE∥BC,
∴$\frac{AD}{BD}=\frac{AE}{CE}$=$\frac{2}{1}$,
∴$\frac{AE}{AC}$=$\frac{2}{3}$,
∴$\frac{{S}_{△ADE}}{{S}_{△ADC}}$=$\frac{2}{3}$,
∴S△ADE=$\frac{2}{3}$S△ADC,
∵$\frac{AD}{BD}$=$\frac{2}{1}$,
∴$\frac{{S}_{△ADC}}{{S}_{△BDC}}$=2,
∴S△BDC=$\frac{1}{2}$S△ACD,
∴S△ADE:S△BDC=$\frac{4}{3}$.
点评 本题考查了平行线分线段成比例,熟练掌握等高不同底的三角形的面积的比等于底的比是解题的关键.

练习册系列答案
相关题目
4.我们居住的地球的半径约为6400千米,这里的“6400”属于( )
| A. | 记数 | B. | 测量结果 | C. | 标号 | D. | 排序 |
 在△ABC中,AB=AC,AD⊥BC于D,DF⊥AB于F,AE⊥CF于E且交DF于M,求证:M为DF的中点.
在△ABC中,AB=AC,AD⊥BC于D,DF⊥AB于F,AE⊥CF于E且交DF于M,求证:M为DF的中点.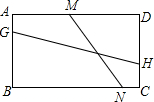 如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$.
如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$.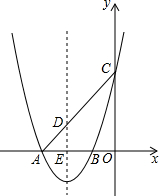 如图,抛物线y=x2+4x+3交x轴于A,B两点(A在B左侧),交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+4x+3交x轴于A,B两点(A在B左侧),交y轴于点C.已知一次函数y=kx+b的图象过点A,C.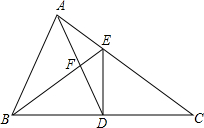 如图,△ABC中,D、E分别为BC、AC上一点,AB=AD,BE=EC.
如图,△ABC中,D、E分别为BC、AC上一点,AB=AD,BE=EC.