题目内容
17.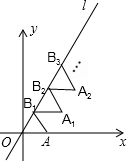 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2014的坐标是(1007,1007$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2014的坐标是(1007,1007$\sqrt{3}$).
分析 根据题意得出直线BB1的解析式为:y=$\sqrt{3}$x,进而得出B,B1,B2,B3坐标,从而得出坐标变化规律,进而得出答案.
解答 解:如图,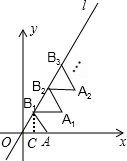
过B1向x轴作垂线B1C,垂足为C,
∵△OAB1是边长为1的等边三角形,
∴OB1=1,∠B1OC=60°,
∴∠OB1C=30°,
∴OC=$\frac{1}{2}$OB1=$\frac{1}{2}$,CB1=OB1sin60°=$\frac{\sqrt{3}}{2}$,
∴B1的横坐标为:$\frac{1}{2}$,则B1的纵坐标为:$\frac{\sqrt{3}}{2}$,
∴B1的坐标为:($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∵点B1,B2,B3,…都在直线y=$\sqrt{3}$x上,
同理可得出:B2的横坐标为:1,则B2的纵坐标为:$\sqrt{3}$,
∴B2(1,$\sqrt{3}$),
…
Bn($\frac{n}{2}$,$\frac{\sqrt{3}n}{2}$).
∴点B2014的坐标是(1007,1007$\sqrt{3}$).
故答案为:(1007,1007$\sqrt{3}$).
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
7.化简:$\frac{{x}^{2}}{{x}^{2}+4x+4}$÷$\frac{x}{x+2}$=( )
| A. | x | B. | $\frac{1}{x+2}$ | C. | $\frac{x}{x+2}$ | D. | x+2 |
5. 如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )
如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )
 如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )
如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | 12 | D. | 24 |
7.某区10名学生参加市级汉字听写大赛,他们得分情况如表:
那么这10名学生所得分数的众数和中位数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和85 | B. | 85和80 | C. | 95和85 | D. | 85和87.5 |