题目内容
在△ABC中,已知∠A、∠B、∠C的对边a、b、c满足a+c=2b,且∠C=2∠A,求sinA的值.
考点:三角形边角关系
专题:计算题
分析:延长AC到D,使CD=CB=a,作BE⊥AD于E,如图,由CB=CD=a得∠CBD=∠D,根据三角形外角性质得∠ACB=2∠D,易得∠A=∠D,则BA=BD=c,而BE⊥AD,根据等腰三角形的性质得AE=
(a+b),在Rt△ABE中,根据余弦的定义得cosA=
=
,加上余弦定理cosA=
,得到
=
,整理得c2-a2=ab,然后把c=2b-a代入可计算得a=
b,则c=
b,接着可计算出cosA=
,最后利用同角的正弦和余弦的关系求∠A的正弦值.
| 1 |
| 2 |
| AE |
| AB |
| a+b |
| 2c |
| b2+c2-a2 |
| 2bc |
| b2+c2-a2 |
| 2bc |
| a+b |
| 2c |
| 4 |
| 5 |
| 6 |
| 5 |
| 3 |
| 4 |
解答:解:延长AC到D,使CD=CB=a,作BE⊥AD于E,如图,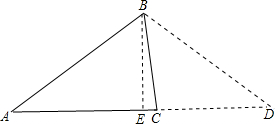
∵CB=CD=a,
∴∠CBD=∠D,
∴∠ACB=2∠D,
∵∠ACB=2∠A,
∴∠A=∠D,
∴BA=BD=c,
而BE⊥AD,
∴AE=
AD=
(a+b),
在Rt△ABE中,cosA=
=
=
,
∵cosA=
,
∴
=
,
∴c2-a2=ab,
∵a+c=2b,
∴c=2b-a,
∴(2b-a)2-a2=ab
∴a=
b,
∴c=2b-
b=
b,
∴cosA=
=
,
∴sinA=
=
=
.

∵CB=CD=a,
∴∠CBD=∠D,
∴∠ACB=2∠D,
∵∠ACB=2∠A,
∴∠A=∠D,
∴BA=BD=c,
而BE⊥AD,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABE中,cosA=
| AE |
| AB |
| ||
| c |
| a+b |
| 2c |
∵cosA=
| b2+c2-a2 |
| 2bc |
∴
| b2+c2-a2 |
| 2bc |
| a+b |
| 2c |
∴c2-a2=ab,
∵a+c=2b,
∴c=2b-a,
∴(2b-a)2-a2=ab
∴a=
| 4 |
| 5 |
∴c=2b-
| 4 |
| 5 |
| 6 |
| 5 |
∴cosA=
| ||
2×
|
| 3 |
| 4 |
∴sinA=
| 1-cos2A |
1-(
|
| ||
| 4 |
点评:本题考查了三角形的边角关系:等边对等角;三边三角满足余弦定理和正弦定理.

练习册系列答案
相关题目
 如图,已知B,C,D三点在同一直线上,CE∥BA,求∠A+∠B+∠BCA的度数.
如图,已知B,C,D三点在同一直线上,CE∥BA,求∠A+∠B+∠BCA的度数.